notdecidedyet

Reasoning model을 Agent활용

Prompt로 서치를 언제할지 컨트롤함: 3.3 Agentic Retrieval-Augmented Generation Mechanism

예시 작성함: Knowledge Refinement via Reason-in-Documents

https://github.com/sunnynexus/Search-o1

Abstract

Large Reasoning Model(LRM)은 뛰어난 추론 능력을 보여주지만, 지식 부족으로 인한 한계가 있음. 이를 해결하기위해 다음과 같은 프레임워크를 제시함.

• Search-o1: LRM을 agentic RAG방법과 Reason-in-documents모듈로 강화
  • 추론 과정에서 search와 통합. 불확실한 지식에서 외부 지식의 동적 검색 가능. 검색된 정보를 심층 분석 후 추론 체인에 주입

Introduction

• LRM의 발전: o1, QwQ, DeepSeekR1등 추론 능력이 뛰어난 모델들이 개발
• LRM한계: 과도한 사고, 지식 부족의 한계가 있음.
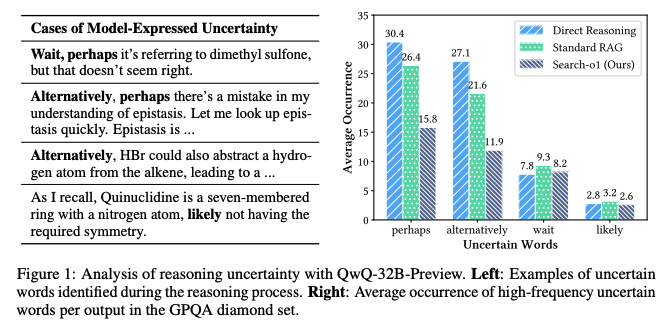
  • 도전적인 문제에서는 perhaps와 같은 불확실한 단어(fig1)를 추론 과정에서 평균 30회 이상 하는 것을 발견함.
  • 이러한 불확실성 및 지식 부족은 오류를 더 크게만들고, 전체 추론 체인을 방해함.
• 제안: Search-o1 - 자율적인 검색을 통해 성능 향상.
  • 표준 RAG:
    • 한계: 관련 지식을 한번 검색
    • 극복: 지식이 부족하면 능동적으로 검색 쿼리 생성.
  • 검색 정보 통합:
    • 한계: 검색된 문서의 중복 처리 문제가 있음. -> Reasoning Model의 Context 제한과 연관 있음.
    • 극복: Reason in documents모듈 도입 - 메인 추론 체인과 독립적으로 검색된 문서 분석 및 정제
• 기여: 
  1. 최초 통합 프레임워크: 추론모델을 agentic search 워크플로우에 통합하여 자율적으로 지식 보완
  2. 효과적 지식 통합: 추론 과정을 agentic RAG 메커니즘과 지식 정제 모델과 결합하여 논리적 흐름 유지
  3. 좋은 성능

Related Work

• Large Reasoning Models
  
  • 전통적 LLM: 모델 크기 확장이나 학습 데이터 확장을 통해 훈련 에서 확장성 달성
  • 추론 모델: 추론에서 확장성을 달성하여 성능 향상
    • o1과 같은 추론 능력 달성 방법:
      • 추론시에서 Monte Carlo Tree Search (MCTS)와 함께 정책 및 리워드 모델 결합
        -> 허나 이는 모델 자체에 추론 능력을 내재화 하는 것은 아님.
      • 훈련 데이터 증류를 통한 능력 향상
    • 한계: 내부 지식이 불충분할 때 외부 세계 지식을 활용할 수 없음
• Retrieval-Augmented Generation (RAG)
  
  • RAG 시스템 향상: 쿼리 전처리, 문서 압축, 노이즈 제거, 정제, 지시 따르기 등
  • 발전된 접근법: 엔드 투 엔드 모델 훈련을 통한 RAG 시스템 구현, 지식 그래프 기반 RAG 시스템
    Agentic RAG 시스템: 모델이 자율적으로 검색 시기와 내용 결정
  • 한계: 기존 RAG 접근법은 o1과 같은 모델의 강력한 추론 능력과 결합되지 않음

Methodology

3.1 Problem Formulation

• 목표: 두가지 요소 생성
  • R: 논리적 추론 체인
  • a: 최종 답변
• 입력: 
  • I: 작업 지시사항(instruction)
  • q: 질문(query, question)
  • D: 검색된 외부 지식(Data)
• 수학적 표현
  • 설계: 입력(I,q,D) -> 출력(R,a)로 매핑을 하는 것
  • 확률적으로 모델링하면 아래처럼 표현 가능
    -> 앞에 있는 수식인 추론 과정을 먼저 생성하고, 이후 Answer부분을 만들어낸다.

3.2 Overview of the Search-o1 Framework

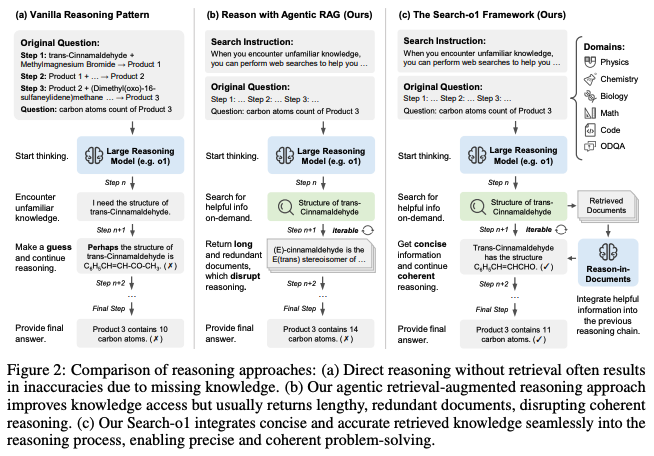
• search-o1 목적: LRM의 지식 부족 문제를 해결하기 위함.
• 세가지 접근 방식: 
  • Vanila Reasoning Pattern(a): 정확한 정보 접근이 어려우면, 모델은 가정에 의존해야함. 연쇄 오류를 발생시킴
  • Agentic RAG(b): 모델이 자율적으로 외부 지식 접근 할 수 있도록함. 그러나 길고 관련없는 정보 포함하면 추론 흐름 방해함.
  • Search-o1(c): agentic RAG확장판, 외부 지식을 통합하며 추론 체인의 논리적 흐름을 유지하며 하는 추론.

3.3 Agentic Retrieval-Augmented Generation Mechanism

• Agentic RAG: 추론 과정 중에 자율적으로 외부 지식을 검색한 시기를 결정할 수 있음.(Appendix A.1)
  • 자율적인 검색 쿼리 생성
    • 조건: 모델이 추론 중 지식이 불확실할 때
    • 구현: <|begin_search_query|> 및 <|end_search_query|> 사이에 검색 쿼리를 생성 
    • 식: (2)
  • 검색 호출
    • 호출 시점: 모델이 <|end_search_query|> 토큰을 생성하는 순간
    • 과정: 추론 일시 중지 -> 검색 쿼리 추출 -> 검색 함수 호출
    • 식: (3)
  • 검색 결과 통합
    • 위치: 특수 기호 <|begin_search_result|> 및 <|end_search_result|> 사이
    • 방법: 추론 체인 $R^{i-1}$에 검색 결과 삽입
    • 처리: 모델이 삽입된 검색 결과를 참고해 추론 계속 진행
  • 정리:
    • 모델이 지식이 부족함을 느끼면
    • <|begin_search_query|>생성
    • 검색하려는 쿼리를 생성
    • <|end_search_query|> 생성
    • <|begin_search_query|>와 <|end_search_query|> 사이에 있는 텍스트를 추출하여 검색 쿼리로 사용
• Search
  • 검색 결과로 나온 i개의 가장 관련있는 문서를 선택하고, <|begin_search_result|>와 <|end_search_result|> 사이에 추론 체인 $R^{i-1}$에 삽입되어, 외부 지식을 활용하여 추론 과정을 계속할 수 있게 함.

3.4 Knowledge Refinement via Reason-in-Documents

• 이 단계의 목적: 
  • 검색된 문서의 정보는 중복: 길고 중복된 정보는 -> 일관성 및 노이즈 들어갈 수 있음.
  • 긴 문서 이해 제한: lost in the middle, limited context length
• 작동방식:
  • 입력: (이전 까지의 추론, 현재 검색 쿼리, 검색된 문서)
  • 처리 방법(Appendix A.1):
    • 중간 추론 시퀀스 생성(식4): retrieve 정보를 추론, 논리 체인의 일관성을 유지하면서 정제된 지식으로 변환
      더보기

      문제: trans-cinnamaldehyde가 methylmagnesium bromide와 반응하여 생성물 1을 형성했습니다. 이후 여러 단계의 반응 후 최종 생성물 3의 탄소 원자 수는 몇 개인가요?
      
      1. 초기 추론 단계:
      이 화학 반응 문제를 해결하기 위해 단계별로 접근해보겠습니다. 먼저 trans-cinnamaldehyde와 methylmagnesium bromide의 반응을 이해해야 합니다. methylmagnesium bromide는 Grignard 시약으로 카르보닐 화합물에 친핵성 공격을 합니다. 그러나 trans-cinnamaldehyde의 정확한 구조를 모르겠습니다
      
      2. 검색 쿼리 생성
      <|begin_search_query|>structure of trans-cinnamaldehyde<|end_search_query|>
      
      3. 검색 결과
      Wikipedia: "Trans-cinnamaldehyde (또는 (E)-cinnamaldehyde)는 분자식 C9H8O를 가진 방향족 알데히드로, 페닐 고리에 연결된 propenal 그룹으로 구성되어 있습니다..."
      화학 교육 사이트: "Trans-cinnamaldehyde의 구조는 페닐 고리(C6H5)가 이중 결합으로 알데히드 그룹에 연결된 형태입니다..."
      
      4. 중간 추론 시퀀스 r_docs생성
      검색된 웹 페이지를 분석해보니, trans-cinnamaldehyde의 구조에 대한 정보를 얻을 수 있습니다. 이 화합물은 분자식 C9H8O를 가지며, 페닐 고리가 이중 결합으로 알데히드 그룹에 연결된 형태입니다. 이 정보는 현재 추론 단계에서 필요한 trans-cinnamaldehyde의 구조를 이해하는 데 도움이 됩니다. 특히 탄소 원자 수가 9개라는 점이 중요합니다
      
      5. 4번의 추론 시쿼스로 -> 정제된 지식 생성 r_final
      (근데 이 과정이 왜 필요한지는 모르겠음)
      Trans-cinnamaldehyde(또는 (E)-cinnamaldehyde)는 분자식 C9H8O를 가집니다. 페닐 고리가 이중 결합을 통해 propenal 그룹에 연결된 구조로, 분자는 평면형입니다. 이 구조는 9개의 탄소 원자, 8개의 수소 원자, 1개의 산소 원자로 구성되어 있으며, 기능기는 화학적 변환에서의 반응성을 나타냅니다.
      
      6. 추론 체인에 통합 (R^1)
      이 화학 반응 문제를 해결하기 위해 단계별로 접근해보겠습니다. 먼저 trans-cinnamaldehyde와 methylmagnesium bromide의 반응을 이해해야 합니다. methylmagnesium bromide는 Grignard 시약으로 카르보닐 화합물에 친핵성 공격을 합니다. 그러나 trans-cinnamaldehyde의 정확한 구조를 모르겠습니다.
      <|begin_search_query|>structure of trans-cinnamaldehyde<|end_search_query|>
      <|begin_search_result|>Trans-cinnamaldehyde(또는 (E)-cinnamaldehyde)는 분자식 C9H8O를 가집니다. 페닐 고리가 이중 결합을 통해 propenal 그룹에 연결된 구조로, 분자는 평면형입니다. 이 구조는 9개의 탄소 원자, 8개의 수소 원자, 1개의 산소 원자로 구성되어 있으며, 기능기는 화학적 변환에서의 반응성을 나타냅니다.<|end_search_result|>
      이제 trans-cinnamaldehyde의 구조를 알았으니, 반응을 계속 분석할 수 있습니다. Trans-cinnamaldehyde는 9개의 탄소 원자를 포함합니다. Methylmagnesium bromide가 알데히드 카르보닐 그룹을 공격하면 메틸 그룹(-CH3)이 추가되어 생성물 1에는 10개의 탄소 원자가 포함됩니다...
      
      

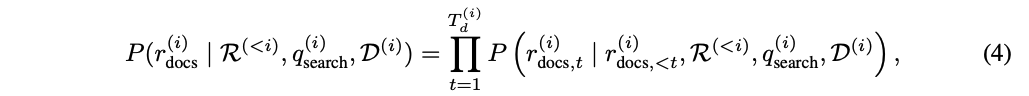
3.5 Search-o1 Inference Process

• 단일 질문에 대한 추론 로직:
  1. 초기화: 지시사항(I), 질문(q)를 연결해 초기 인풋 생성
  2. 추론 및 검색 쿼리 생성: 1의 인풋으로 추론 체인 R생성 시작. 지식이 부족하면 모델이 자율적으로 특정 토큰 생성.
  3. 검색 수행: <|end_search_query|> 태그 감지 시 추론 일시 중지, 검색 쿼리 추출, 외부 검색 및 문서(D)획득
  4. 문서 정제: Reason-in-Documents모듈로 검색 문서 정제 -> r_ifnal생성
  5. 정제된 정보 통합: r final을 <|begin_search_result|> 및 <|end_search_result|> 태그 사이에 삽입, 추론체인 R에 통합.
  6. (2-5)과정을 필요에 따라 반복함.
• 배치 추론 메커니즘: 여러 질문을 동시에 처리하기 위함: 자세한 설명 생략

Experiments

4.1 Tasks and Datasets

• 수학 과학, 코딩 문제: GPQA, MATH500, AMC2023, AIME2024, LiveCodeBench
• 오픈 도메인 QA

4.2 Baselines

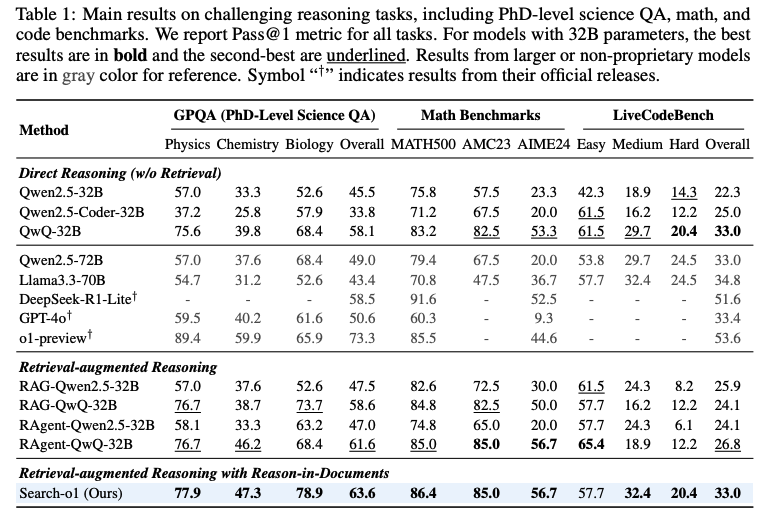
• Direct Reasoning (w/o Retrieval)
• RAG Reasoning: 
  • Standard RAG: 10개 문서 검색하고, 추론 및 답변 생성
  • RAgent(RAG Agent): 검색 시점을 모델이 결정할 수 있 함. 검색된 문석의 길이를 관리하기 위해 ReAct에서 영감을 받아 추론 중에 먼저 상위 10개 스니팻을 검색함.
  • Search-o1: QwQ-32B를 사용
• 눈여겨볼 것: Query에 모든 정보가 있는 Math는 QwQ-32B나 Search-o1이나 큰 성능차이가 없음. 허나 GPQA같은 경우는 성능차이가 유의미하게 나타나보임.

4.3 Implementation Details

• 모델: Search-o1의 백본으로 오픈 소스 QwQ-32B-Preview 사용
• 설정: 최대 32,768 토큰, 온도 0.7, top_p 0.8, top_k 20, 반복 패널티 1.05
• 검색 설정:Bing Web Search API 사용 (US-EN 지역 설정), 상위 10개 문서 검색, Jina Reader API로 웹 페이지 내용 가져오기
• 추가 전략:
  • 최종 답변 미제공 시 직접 추론 결과를 사용하는 백오프 전략 적용
  • Non reasoning 모델에는 간단한 Chain-of-Thought 프롬프팅 적용

4.4 Results on Challenging Reasoning Tasks

• Main Result
  • QwQ-32B-Preview의 우수성: instruction LLM보다 일관되게 성능 우수
  • RAgent-QwQ-32B의 장점: 대부분의 작업에서 표준 RAG 기반 모델과 직접 추론 QwQ-32B 모두 능가.
  • Search-o1의 성능: Reason-in-Documents 전략으로 외부 지식을 통합하면서 원래 추론의 일관성 유지. 
• Scaling Analysis on Number of Retrieved Documents.
  • 효과적인 문서 활용: Search-o1은 검색된 문서 수가 증가함에 따라 복잡한 추론 작업 성능 향상
  • 단일 문서의 효율성: 단 하나의 문서만 검색해도 10개 문서를 사용하는 직접 추론 및 표준 RAG 모델 능가
  • 도메인별 성능: 물리학, 화학, 생물학, 전체 성능 모두에서 검색 문서 수 증가에 따른 일관된 개선
  • Agentic search와 Reason-in-Documents 전략의 효과 확인

3.2. 성능 저하 없는 LoRA finetuning(표1): LongCoT를 증류하는 것이 효과적인지 조사함. 과거 연구에 따르면 LoRA는 full finetuning보다 성능이 떨어진다고 하였으나, LoRA fine-tuning이 수학 및 코딩 벤치마크 전반에 full SFT와 비슷하거나 더 우수한 성능을 보임.
-> LongCoT의 능력은 지식 습득에 의존하기보다, 구조화된 추론 패턴을 학습하는데 의존할 수 있음.
-> 따라서 LoRA에서 작동을 잘함.
-> LoRA를 통해 새로운 지식을 배우는것은 효과적이지 않다고 알려져있음.

4.1 Wrong or Corrupted Local Content: 로컬 내용의 오류는 모델 성능에 미미한 영향을 끼침

4.2

최종 솔루션만 제공하는 것으로는 강한 추론 능력 학습 불가

단계 간 논리적 연속성이 중요함. 단순한 단계 증가는 효과 없음.

5.1 SFT+LoRA할 경우 Catastrophic forgetting피할 수 있음.

5.4 Best-of-N에서 제대로 된것을 선택할 수 있다면, 엄청 강력하네...

Abstract

• Long CoT는 reflection, backtracking, self-validation을 포함하나, 어떻게 효과적으로 학습시키는지 어떤 데이터가 필요한지 명확하게 이해되지 않았음.
• 발견1: LLM이 적은 데이터 및 LoRA로 LongCoT를 배울 수 있음을 발견함.
  • Qwen2.5-32B-Instruct + 17K 학습후 AIME 56.7%성능 달성
• 발견2: 구조가 내용보다 중요하다는 것을 발견.
  • 잘못된 답변이 포함된 샘플로 훈련해도 성능 하락이 미미함(3.2%)
  • 숫자를 무작위로 바꾸거나 추론 키워드를 제거해도 성능에 큰 영향이 없음.
  • 추론 단계 순서를 섞거나 단계를 삭제하면 성능이 크게 하락함

Introduction

• LRM들은 Long CoT를 통해 복잡한 추론 문제를 해결, 그러나 기존 방법은 공개되지 않거나 비쌈.
  -> Long CoT능력을 개발하는 방법은 아직 불명확함
• 적은 데이터 및 적은 웨이트만 학습해도 추론 능력을 크게 향상시킬 수 있음을 보여줌.
  • LoRA fine-tuning을 통해 5% 미만의 파라미터를 업데이트하여 o1-preview의 성능을 달성할 수 있다. 모델이 중간 생각을 반영하고 수정하는 것을 성공적으로 배우고(예: "Alternatively"와 "Wait, but"와 같은 추론 키워드를 자주 사용) 어려운 문제를 해결하기 위해 길고 일관된 CoTs를 사용하는 것을 보여준다(그림 1)

Related Work

• Test Time Scaling for Large Language Models: 
  • Single Long CoT: 모델이 하나의 긴 CoT를 생성하도록 훈련
    • 모델: o1, R1, QwQ
    • 작동방식: in context reflection, backtracking통한 추론
  • Repeatedly Sampled CoT: 모델에서 여러번 응답 생성해 최적의 답을 선택하는것
    • 방법: BoN, MCTS 등. 검색 및 Reward모델로 다수 응답 생성
• Training to Improve Reasoning Capabilities of LLMs:
  • 직접적인 훈련을 통해 LLM의 추론 능력을 향상 시키는 방법
    • 방법: 모델이 스스로의 출력을 개선하도록 훈련. (강화학습)
    • 논문: Tulu-3, PRIME, R1
• Distillation

Simple Distillation is effective

소량의 데이터 및 LoRA만으로 추론 능력을 효과적으로 향상시킬 수 있음을 보여줌

3.1 Experiments Setup

• R1, QwQ-32B-Preview로 증류 데이터 생성.
• 데이터: AIME, Math등에서 어려운 문제들을 선별
  -> GPT-4o-mini사용하여 선별.
  -> 수학 문제의 경우 정확한 매칭을 통해, 코딩 문제의 경우 코드 실행을 통해 정답과 대조함.
  -> 총 12k의 수학문제, 5k의 코딩 문제를 QwQ의 정확한 응답으로 데이터 구성
  -> 또 다른 데이터로, 공개된 R1-17k reasoning데이터셋 사용
• 모델: Qwen2.5-32B-Instruct
• Object Function: NextTokenPrediction
• 실험: 전체 파라미터 튜닝, LoRA파인튜닝.

3.2 Key Insights

• 적은 양의 데이터로 충분: 그림1(b)에서 17k(R1) 데이터로 파인튜닝 성능을 보여주는데, SFT, LoRA모두 LongCoT를 배우고, 단 16k 훈련 샘플만으로 모든 벤치마크에서 크게 향상됨.
• 성능 저하 없는 LoRA finetuning(표1): LongCoT를 증류하는 것이 효과적인지 조사함. 과거 연구에 따르면 LoRA는 full finetuning보다 성능이 떨어진다고 하였으나, LoRA fine-tuning이 수학 및 코딩 벤치마크 전반에 full SFT와 비슷하거나 더 우수한 성능을 보임.
  -> LongCoT의 능력은 지식 습득에 의존하기보다, 구조화된 추론 패턴을 학습하는데 의존할 수 있음.
  -> 따라서 LoRA에서 작동을 잘함.
  • 7k의 QwQ샘플 + LoRA 모델이 17k QwQ distilled샘플로 훈련된 모델과 비슷함. 그림 1a에서 보듯, LoRA fine-tuned모델은 reflection, self-verification을 통해 LongCoT응답을 생성하는 방법을 쉽게 배움.

4. Long CoT: Structure Is The Key

적은 수의 데이터로 추론 성능이 크게 향상되는 이유를 조사한다.

• local content : 최종 답변의 정확성, 수학 도출에서 숫자의 중요성, 추론 키워드들의 중요성
  -> 검증: 이에 해당하는 내용들을 변형. (1+1=3과 같이 틀린 내용으로 변형)
• global reasoning : reflection, self-verification, backtracking을 포함하는 구조
  -> 검증: 추론 구조를 수정. 셔플링, 삽입, 삭제 등
• 결론: local content에는 관대하나, global reasoning에는 매우 민감함.

4.1 Wrong or Corrupted Local Content: 로컬 내용의 오류는 모델 성능에 미미한 영향을 끼침

• 정답이 틀린 샘플로 훈련: 정확한 샘플 대비 -3.2%하락(엄청 큰 하락은 아니였음)
• 수학 풀이 과정의 숫자 무작위로 대체: 70%의 숫자 손상 62%정확도 -4.3%. 100%의 숫자 손상 2.7%정확도
  -> 일부 풀이 과정이 손상되는것은 큰 영향이없다.
• 추론 키워드 제거: Wait, Alternatively제거 -> 모든 키워드 제거해도 63%의 정확도 달성

4.2 Corrupted Global Reasoning Structure(fig 3)

• 추론 단계 삭제: 추론단계의 33%, 67%, 100% 삭제
  • 결과: 삭제 비율에 따라 선응이 꾸준히 감소함.
  • 결론: 최종 솔루션만 제공하는 것으로는 강한 추론 능력 학습 불가
• 추론 단계 삽입: 원래 추론 단계를 다른 문제의 추론 단계로 33%, 67%, 100% 대체
  • 결과: 응답 길이와 키워드 사용은 증가했으나, 정확도는 하락함. 각 단계는 개별적으로 일관성이 있으나 전체적인 논리 연결이 부재함. 존재하지 않는 이전 단계를 참조하거나, 일관성이 없는 케이스 열거 등 문제가 발생함.
  • 결론: 단계 간 논리적 연속성이 중요함. 단순한 단계 증가는 효과 없음.
• 추론 단계 셔플: 추론 단계의 순서를 무작위로 재배열 (33%, 67%, 100%)
  • 결과: 응답 길이, 키워드 사용 증가하나 정확도는 크게 하락함. 92% 이상의 응답이 이전 맥락 없이 Alternatively, Wait으로 시작함. 이전에 언급되지 않은 계산이나 케이스 참조 현상 발생
  • 결론: 단계간 논리적 흐름 필수

5. Ablation

5.1 Performance on Non-Reasoning Benchmarks: Long CoT 데이터로 fine-tuning을 하면 비추론 작업에서 성능이 저하되나?

QwQ는 비추론 데이터셋에서 성능하락이 보임

반면 SFT+LoRA할 경우 모든 데이터셋에서 큰 성능 하락이 없음.

SFT+LoRA할 경우 Catastrophic forgetting피할 수 있음.

5.2 Effect on Different Student Models: 

모델 8개중 7개가 퍼포먼스가 향상됨. 허나 Qwen2.5-32B만큼의 성능 향상이 있지는 않음.

5.3 Comparison to Best-of-N: BoN에서 생성된 데이터에서 적절하게 잘 선택할 수 있다면 매우 강력함.

BoN으로 성능향상이 큰 모델의 경우, LongCoT로 파인튜닝한 모델의 성능도 성능향상이 컸다.

Llama3.1 8B의 경우 Best-of-8을 해도 10% 미만의 정확도를 보임
-> LongCoT를 해도 성능 향상이 낮음.

https://jihoonjung.tistory.com/176

선호도 데이터셋을 아래와 같이 구하는것은 적용해볼만한 방법인 것 같다.

github: https://github.com/Gen-Verse/ReasonFlux

Abstract

• 위계적(hierachical) LLM 추론을 통해 추론 검색 공간을 효율적으로 최적화
• 세가지 특징
  • 구조화되고 일반적인 reasoning 템플릿 라이브러리: 유사하거나 관련된 추론 문제로 일반화 가능한 약 500개의 고수준 사고 템플릿 포함
  • 위계적 강화 학습: 원래 긴 CoT 데이터 대신 reasoning 템플릿 시퀀스에 대해 위계적 강화 학습 수행하여, 복잡한 문제를 점진적으로 처리하기 위한 최적 템플릿 궤적을 계획하도록 LLM을 최적화 시킴
  • 추론 확장 시스템 : 추론시 reasoning 템플릿을 적용해 위계적 LLM추론을 가능하게 하는 추론 확장 시스템 제안

1. Introduction

• 기존 연구 한계 : 신중한 검색과 보상 모델 안내 방법으로 나뉨
  • 신중한 검색 (ToT, GoT): 여러 추론 경로 탐색 및 자체 평가를 통한 최적 궤적 찾기
  • 보상 모델 안내 (Best-of-N, PRM, MCTS): 보상 모델 활용하여 추론 단계 품질 평가 및 유망한 경로 안내
  • 한계 : 높은 계산 비용, 최적 추론 궤적 식별 어려움, 수동 설계된 검색 전략 및 인스턴스/단계 수준 보상에 의존, 일반화 능력 제한, 탐색-활용 트레이드오프 균형 유지 어려움
• 템플릿 기반 추론의 한계:
  • 템플릿 기반: RAG 활용 (BoT, SuperCorrect)
  • 한계: 한 문제를 풀 때, 여러 샘플들을 불러오고 정보의 일부분만 적용해야 함

2. Related Work

• Learning from Preferences for Language Models: LLM을 인간의 기대와 인식에 맞게 조정하는 데 필수적
  (Step-DPO와 Cross-DPO처럼 중간 추론이나 반성 단계를 대상으로 하는 더 세밀한 최적화에 초점)
  한계 : 기존 방법들은 인스턴스나 일부 보상에 의존함. 인간 처럼 (해결하는 과정에 포함된)높은 수준의 인지 과정을 포착하지 못함.
  • 이 연구에서는: RL기반 최적화를 도입. 고수준 reasoning 템플릿을 구성하도록 모델을 encourage함.
• Retrieval-Augmented Generation for Language Models:
  • 장점 : 대규모 외부 지식 소스에서 관련 문서 검색하여 응답 생성 정보 제공, 질문-답변에서 뛰어난 성능, 적은 매개변수로도 우수한 성능 달성 등
  • 단점 : 수학과 코드와 같은 복잡한 추론 작업에서 어려움 발생, 표준 임베딩 유사성 검색을 통해 관련 가이드라인이나 템플릿 검색 어려움
  • 이 연구에서는: 복잡한 추론 문제를 대상으로 효율적이고 정확한 검색을 위한 구조화되고 컴팩트한 템플릿 라이브러리 설계
• Inference Scaling for LLM Reasoning: 복잡한 문제 해결을 위해 더 많은 토큰 생성 필요.
  • 기존 연구 : CoT, ToT, GoT, Best of N, MCTS, PRM, BoT.
  • 한계 : 템플릿 기반 접근법에 대한 탐색-활용 트레이드오프에 대한 깊은 이해 부족
  • 이 연구에서는: 복잡한 작업에 대한 추론 정확도를 크게 향상시키면서 탐색과 활용 간의 전략적 균형을 맞추는 위계적 템플릿 RAG

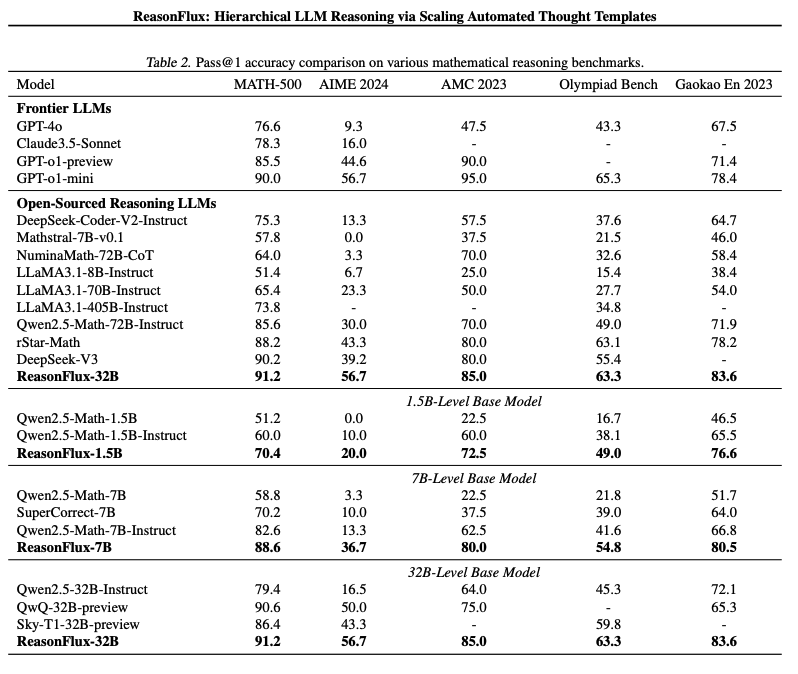
3. ReasonFlux: Scaling Thought Templates for Hierarchical LLM Reasoning

3.1 Constructing Structured Thought Template Library

• 배경:
  • RAG: 인간이 복잡한 추론 문제 해결 시 외부 자원을 찾으며 해결하는 것에서 영감을 받음.
  • BoT: LLM추론을 위한 높은 수준의 reasoning 버퍼 생성 및 효율적인 RAG추론 시스템 구축 시도. 종합적인 템플릿 라이브러리를 구축해 문제를 해결하려 해도, 템플릿 크기 문제가 있음.
• 이 연구는: 명확한 검색이 가능하도록하고, 확장성 문제를 완화하는 템플릿 구성(structured thought template library)
  • 도전적인 수학적 추론 문제들을 선택: 강건성, 광범위한 적용 가능성을 보장하기 위해
  • 내용:
    • LLM을 사용해 (명시적 해결책 뒤에 있는)reasoning 과정을 분석.
    • 문제 해결 전략의 간결한 요약을 생성.
    • 공통된 패턴 식별
  • 템플릿 예: name, tag, description, scope, application step들로 구성되어 있음.
    검색은 tag, name을 활용

3.2. Hierarchical Reinforcement Learning on Thought Template Trajectory

• 훈련: 이 라이브러리를 활용하여 문제를 해결하기 위한 방법을 배우기 위해 모델을 훈련함.
  • 위게적 강화학습 수행 -> ReasonFlux
• Structure-based Finetuning: LLM이 템플릿의 이름과 태그를 보고 그 템플릿의 설명과 적용 범위를 생성할 수 있도록 훈련
  • 데이터: 구조화된 템플릿 $D_{temp}$에서 훈련 데이터셋 $D_{train}$구성.
    예) ($T_{name}, T_{tag}, T_{des}, T_{sco}$)
  • 훈련: $L_{struct} = -E_{D_{train}}[logπ(T_{des},T_{sco} | T_{nam}, T_{tag}]$
    -> next token prediction의 변형. 이름과 태그로 설명 및 scope을 예측하도록 훈련
• Preference Learning on Thought Template Trajectory: 
  • 파인튜닝 모델: 파인튜닝된 LLM인 πstruct는 입력 문제를 분석하고 적절한 사고 템플릿 시퀀스를 계획
    -> 입력 문제를 분석하고 적절한 템플릿 시퀀스를 계획하는 것을 직접적으로 훈련하지는 않았음... 논문에서 비약이 있는 듯?
    -> 혹은 preference 파인튜닝을 했는데 언급을 안했나?
  • 궤적 생성:
    • 문제 x가 주어지면, πstruct는 문제의 수학적 특성을 분석 -> 사고 템플릿 시퀀스(궤적) $T_{traj} = {s_1, s_2, ..., s_n}$을 계획(각 단계 $s_i는 라이브러리에서 검색된 특정 템플릿 T_i와 연결된다.$)
  • 인스턴스 만들기:
    • LLM은 각 템플릿에 입력 문제 x에 맞춰 적당한 구체적인 문제를 만듬.
    • 더보기

      추상 템플릿:
      1. 피적분 함수 f(x) = √(R²-x²)에서 R 값을 식별
      2. x = R·sin(θ) 치환을 적용
      3. dx = R·cos(θ)dθ로 변환
      4. √(R²-x²) = √(R²-R²sin²(θ)) = √(R²(1-sin²(θ))) = √(R²cos²(θ)) = R·|cos(θ)|로 변환
      5. 적분을 θ에 대한 적분으로 재구성
      
      인스턴스 템플릿:
      1. 피적분 함수 √(4-x²)에서 R=2 확인
      2. x = 2·sin(θ) 치환 적용
      3. dx = 2·cos(θ)dθ 변환
      4. √(4-x²) = √(4-4sin²(θ)) = √(4cos²(θ)) = 2·cos(θ) (θ ∈ [-π/2, π/2]에서 cos(θ) ≥ 0)
      5. 따라서 적분은 ∫√(4-x²) dx = ∫2·cos(θ) · 2·cos(θ)dθ = ∫4cos²(θ)dθ
      
      
      실제 문제 해결:
      ∫√(4-x²) dx = ∫4cos²(θ)dθ = ∫2(1+cos(2θ))dθ = 2θ + sin(2θ) + C
      
      이제 θ를 x로 다시 표현해야 합니다.
      sin(θ) = x/2이므로, θ = arcsin(x/2)
      또한 삼각함수 공식에서 sin(2θ) = 2sin(θ)cos(θ) = 2·(x/2)·cos(θ) = x·cos(θ)
      
      cos(θ) = √(1-sin²(θ)) = √(1-(x/2)²) = √(4-x²)/2
      
      따라서 sin(2θ) = x·√(4-x²)/2
      
      최종적으로:
      ∫√(4-x²) dx = 2·arcsin(x/2) + x·√(4-x²)/2 + C
• 주어진 궤적의 일반화 능력을 평가하기 위해, 아래와 같은 식을 통해서 일반화 성능을 측정. 문제x와 비슷한 문제들의 집합을 불러오고, 추 생성된 궤적을 활용해 각 유사문제를 풀고, 정확도가 보상이 된다.
  -> 보상: 이 궤적이 얼마나 좋은지 측정하는 품질 값으로 사용된다.
  -> 여기서 나오는 inf모델은 Qwen2.5-32B-Instruct

• 선호도 쌍 구성:
  • 모델 출력 샘플링을 여러개하고, 여러개의 다른 템플릿을 생성함.
  • 각 궤적에 대해 R(Traj)을 계산함
  • (x, 더 높은 보상의 궤적, 더 낮은 보상의 궤적) 데이터셋을 구성함
  • 아래와 같이 DPO와 비슷한 Loss function으로 모델을 훈련함.

3.3 Inference Scaling with Scaling Thought Templates

3.1, 3.2과정이 끝난 모델을 ReasonFlux로 명명함. 

• 사고 템플릿 확장(추론 확장 제안): 추론 확장: MCTS, BoN과 같은 방법
  1. 문제x에 대해서 ReasonFlux는 최적의 궤적을 생성함. 
     $T*_{traj} = {s*_1, s*_2, s*_3, ... }$
     이때 궤적에 있는 s_i는 효율적인 검색을 위해 특정 템플릿 이름, 태그와 연관된다.
  2. ReasongFlux로 관련 있는 템플릿 불러옴 : $T_{rag} = ReasonFlux({T^i_{nam}, T^i_{tag}}^n_{i=1}, D_{temp})$
     i=1~n까지로 되어 있는데, ReasonFlux가 생성한 궤적n에 대응하는 템플릿임.
  3. inf모델로 하여, 각 단계 s_i와 템플릿을 참고해, 문제x에 맞게 인스턴스화함. 
     $ŝ_i = π_{inf}(x_i, s_i, T_i)$
  4. $ŝ_i$는 ReasonFlux에 평가되고 분석됨.
     $δ_i = ReasonFlux(T_{traj}, ŝ_i)$
  5. 평가된 분석에 기반해, ReasonFlux는 궤적을 조정할지 여부를 결정함. 후속 단계를 조정하거나 대안이 되는 템플릿을 검색함.
     -> 조정하는 것은 ReasonFlux가 배우지 않았는데, 이게 가능한가?
     -> agent처럼 작동하는것으로 보임. ReasonFlux는 어떤 방향으로 풀어나가는것이 좋다 라는 지식을 배웠으니, 매 스탭마다 생성을 멈추고, ReasonFlux보고 궤적을 수정하도록 하는것으로 보임.

4. Experiment

3.4 정확한 trajectory만 있다면 reasoning 모델을 만들 수 있음.

-> 결과의 정확성보다 인지적 행동의 존재가 더 중요하다는 것을 시사

github : https://github.com/kanishkg/cognitive-behaviors

데이터 생성하는 방법도 참고해 볼 수 있음.

Abstract

• Test Time Compute으로 성능 향상을 이루었음(인지적 행동을 보임). 인지적 행동은 네가지로 나뉨.
  • 검증(verification)
  • 백트래킹(backtracking)
  • 하위 목표 설정(subgoal setting)
  • 역방향 연쇄(backward chaining)
• TTC는 강화학습으로 달성하나, 일부 모델은 잘 작동안함.
  • Qwen은 추론 행동을 보이는 반면, Llama는 그렇지 아니함.
• 허나 적절한 추론 패턴을 포함한 데이터셋을 기폭재로 제공하면 Llama도 Qwen에 버금가게 개선이 가능하다는 것을 발견함.

1. Introduction

• 인간은 어려운 문제를 해결할 때 심사숙고함 -> RL로 훈련한 언어 모델도 유사한 추론 행동을 보임.
• 연구 목적: 언어 모델이 자기 개선을 하는 이유 및 핵심 인지적 행동에 초점을 맞추는 것을 목적으로 함.
• 연구 내용 : 
  • Qwen2.5-3B, Llama-3.2-3B Countdown에서 강화학습으로 훈련해 비교 분석함.
    Qwen상당히 좋아짐 반면 Llama는 제한적인 성과를 보임.
  • 문제 해결에 유용한 인지적 행동을 분석하는 프레임워크 개발
    • 검증, 백트래킹, 하위 목표 설정, 역방향 연쇄(backward chaining)
• 실험 결과 : 
  • Llama 모델에 백트래킹을 포함한 합성 추론 궤적을 유도하여 강화학습 훈련 시 성능 개선 확인.
  • 잘못된 해결책(틀린 답)으로 유도된 경우에도 적절한 추론 패턴을 보이면서 성능 개선이 지속됨을 확인.
  • OpenWebMath에서 추론 행동을 강조하는 데이터를 선별하여 Llama 모델의 성능 개선 유도.

2. Related Work

추론을 강화하기 위한 방법으로 아래와 같은 연구들이 있었음.

1. 외부 검색
   • 추론 궤적 search, 병렬 샘플링, PRMS
     -> 일반적으로 중복 탐색으로 효율성이 나쁨.
2. In-Context Search and Self-Improvement
   
   • ICL, finetuning on linearized search trace, training on self-correction examples
     -> 자기 수정과 백트래킹처럼 원하는 행동을 취하기 위해 훈련 데이터를 잘 엔지니어링이 해야하는 경우가 많음.
3. 강화학습
   • On-policy, off-policy -> 추론 궤적에서 신용 할당(credit assignment)에 대한 접근 방식에 차이가 있음.
   • R1에서 GRPO만으로도 추론 능력을 보임.
     -> 그러나 왜 일부 모델은 RL을 통해 성공적으로 학습하는 반면 다른 모델은 개선에 실패하는지 답을 한 연구는 없음.

3. Method

3.1 Initial Investigation: A tale of two models

• 실험 설정 : 
  • 데이터: Countdown 게임을 테스트베드로 사용 (수학 퍼즐: 주어진 숫자와 연산으로 목표 숫자 만들기).
  • 모델 : Qwen-2.5-3B, Llama-3.2-3B
  • Object : PPO -> 더 안정적이라 선택 (GROP, REINFORCE로 해도 비슷한 결과)
    • PPO 알고리즘으로 250단계 훈련 (프롬프트당 4개의 trajectory 샘플링).
  • 구현 : VERL 라이브러리 및 TinyZero 구현을 활용하여 강화 학습 실험 수행.
• 결과: 
  • Qwen은 30단계 이후 급격한 성능 향상보임, 반면 Llama는 성능향상 미비(Figure1)
  • Qwen은 훈련 후반에 명시적 검증에서 암묵적 해결책 확인으로 전환하는 행동 변화를 보임
    명시적 검증 예) 8*35는 280이고 너무 높습니다.
    암묵적 해결 예) 단어를 사용하지 않고 올바른 답을 찾을 때까지 순차적으로 다른 해결책을 시도함
• Question : 
  • 성공적인 추론 기반 개선을 가능하게 하는 기본적인 능력은 무엇인가?
  • 인지적 행동을 분석하기 위한 체계적인 프레임워크가 필요하다.

3.2 A Framework for Analyzing Cognitive Behaviors

• 먼저 인지적 행동을 정의함 : 정의함으로서 모델 출력에서 인지적 행동을 식별할 수 있음.
  • 4가지
    • 백트랙킹 : 오류 감지 시 풀이 과정을 명시적으로 수정함
    • 검증 : 중간 결과 확인
    • 하위 목표 설정 : 복잡한 문제를 여러 단계로 분할
    • 역방향 chain: 결과에서 입력으로 역으로 추적함 (75에 도달하기 위해, 나눌 수 있는 숫자 필요)
  • GPT-4o-mini를 사용해 모델 출력에서 이러한 패턴을 식별하는 파이프라인 개발

3.3 The Role of Initial Behaviors in Self-Improvement

• Qwen의 성능 향상은 검증 및 백트래킹을 중심으로 발현됨. (그림1의 중간 밑 부분)
• 반면 Llama는 없었음.
• 훈련 전 모델로 비교
  • Qwen-2.5-3B: 네 가지 행동 모두 비율이 Llama 변형보다 높음 (그림 4).
  • Llama-3.1-70B: Llama-3.2-3B보다 행동 활성화 증가, 하지만 불균등 (특히 백트래킹은 제한적).

3.4 Intervening on initial behaviors

인지적인 행동이 중요한 것은 알았음. 근데 그러면 인지적 행동이 발생하지 않는 모델을 어떻게 하면 행동이 발생할 수 있게 하나?

• 데이터셋 준비 : Cluade-3.5-Sonnet으로 CountDown문제 추론 과정 생성
  • 모든 전략 결합(검증, 백트래킹, 하위 목표 설정, 역방향 연쇄 모두 포함)
  • 백트래킹만 포함
  • 백트래킹 + 검증 포함
  • 백트래킹 + 하위 목표 설정 포함
  • 백트래킹 + 역방향 연쇄 포함
  • 빈 chain of thought(아무 인지적 행동 없음)
  • 길이가 일치하는 의미 없는 토큰으로 채워진 chain-of-thought
• 추가 실험
  • 인지적 행동 패턴을 보이는 데이터를 만들지만, 정답이 틀린 데이터셋도 생성
    -> 행동 패턴과, 정확성 중 어느 것이 더 중요한것인지 확인하기 위해서
• 실험 과정
  
  • 파인튜닝 : 각 데이터셋으로 각 모델을 파인튜닝(SFT - Appendix B.Priming)
  • 강화학습 : 파인튜닝 모델들을 PPO 알고리즘을 적용해, CountDown문제 해결 능력 향상시킴.
•  결과 : 
  • Priming with different behaviors: Llama, Qwen파인튜닝후 RL하면 상당한 개선을 보임(Figure 2). 프라이밍을 하게 되면 유용한 행동을 증폭하고, 다른 행동을 억제하는 것을 보임(Figure 3).
    -> 모든 전략 결합한 데이터에서는 백트래킹과 검증은 유지하고 강화하는 반면 역방향 연쇄와 하위 목표 설정은 훈련이 진행될 수록 감소. 억제된 행동(역방향 연쇄와 하위 목표 설정)은 백트래킹과만 짝을 이루었을 때 훈련 전반에 걸쳐 지속

• Testing Behavioral Necessity: empty CoT로 SFT후 훈련 후 결과는 그림5와 같은데, 모델 성능은 Llma기준 30~35%임.
  -> 인지적 행동 없이 추가 토큰을 할당하는 것만으로는 테스트 시간 계산을 효과적으로 사용할 수 없다는 것을 보여줌

• Behaviors versus Correctness: 올바른 행동이지만 정답이 틀린 모델로 훈련된 모델과, 정확한 해결책이 있는 데이터셋으로 훈련된 모델과 동일한 성능을 달성함(그림 6).
  -> 인지적 행동의 존재가 강화 학습을 통한 성공적인 자기 개선을 가능하게 하는 중요한 요소라는 것을 시사함.
  (손상된 추론 궤적에서 학습하는 것을 보여주는 이전 연구(Li et al., 2025)를 확장)
  -> 결과의 정확성보다 인지적 행동의 존재가 더 중요하다는 것을 시사