notdecidedyet

주의 : 본 게시글은 저자가 Recap용으로 작성하는 글로서 명확하지 않은 정의와 모호한 설명이 있을 수 있음.

논문요약

UltraGCN은 Regressive한 메시지 전달을 생략하고, Loss 함수를 통해 무한개의 Message Passing Layer를 통과한 값의 근사치를 구한다. 이를 통해 기존 연구들보다 10배 빠른 수렴 속도를 보이며 산업적으로 적용하는데 무리가 없다.

1. 개론

GCN, GNN계열에서 유저와 아이템간의 high-order 연결을 잘 포착함으로 인해 눈부신 성과를 거두었다. 허나 산업적으로 적용하는데 있어 몇가지 제약 사항들이 존재한다.

GCN계열의 기반 모델은 큰 그래프(large graph)에서 학습하기 어렵기에 산업에서 널리 채택되는데  어려움이 있다. 

- 많은 고객수와 많은 아이템의 갯수로 인해 좀더 효율성과, 확장성에 문제점이 있다. 

- 연구를 통해서 message passing(neighborhood aggregation)에서 많은 시간이 소요됨을 발견하였다.

따라서, 이 연구에서는 message passing에 대한 의문점을 제기하고, 효율적 추천을 위해 message passing이 없는

단순화된 형태의 UltraGCN을 제안한다.

1) Message Passing 과정에서 Edge에 할당되는 가중치는 직관적이지 않아 CF에 적합하지 않을 수 있다

2) Forward를 진행하는데 여러 관계는(사용자-아이템 쌍, 아이템-아이템 쌍, 사용자-사용자 쌍 등) 재귀적으로 결합하지만 다양한 중요도를 포착하지 못한다(학습에 혼란을 주는 노이즈가 및 정보가 없는 관계가 있을 수 있음)

3) OverSmoothing은 LightGCN에서 3개 이상의 Layer를 사용하는데 제약사항을 주었다. 따라서 Encoder를 통해 메시지 전달을 하기보다 Loss를 통해 ultimate 그래프 컨볼루션을 수학적으로 근사치를 구하는 UltraGCN을 제안.

2. GCN, LightGCN 돞아보기

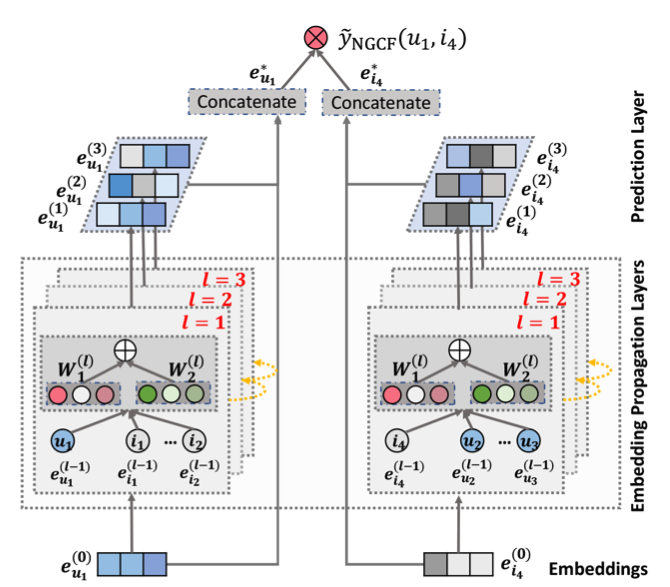
위 그림에서 윗쪽에 있는 부분이 GCN부분이며, 수식으로 표현하면 아래와 같다.

- Sigma : activation

- A : Adjacency Matrix

- D : Diagonal Node Degree Matrix

- A_hat : A + I

- D_hat : D + I

- E : Embedding

- W : Weight

GCN에서 LightGCN으로 변화하면서 Layer를 표현하는 방법은 아래와 같이 바뀌었다.(Self Connect 및 Weight Param제거, 초기의 embedding만 학습 가능). 허나, 임베딩의 가중치 합계를 최종 출력 벡터로 출력하기 때문에 self-loop와 유사한 효과를 내어 아래처럼 표현할 수 있다.

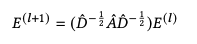
User쪽에서 Layer를 통한 Embedding과정을 자세히 살펴보면 아래처럼 작성할 수 있다.

아래 그림은 User중에 u라는 케이스를 도식화 및 수식화 한것이다.

2.2 Message Passing의 한계점

맨 마지막 레이어에서 User_Emb * Item_Emb을 진행하는데, 3번과 4번 식을 차용해서 표현하면 5오 같은 수식으로 나타낼 수 있다.

이때 알파들은 아래와 같이 표현한다. ( 위 수식을 간단하게 표현하기 위해 알파를 정의함 )

전개된 식을 살펴보면 1)User-Item, 2)Item-Item, 3)User-User 4)(User와 연결된 아이템)-(아이템과 연결된 유저)등의 관계를 포착하는 것을 볼 수 있다. 이때문에 GCN기반 모델이 CF에 효과적인 이유이다. 허나 네가지 유형의 관계에서 할당된 가중치가 CF에서 적합하지 않은 것을 발견하였다.

한계점 1. 가중치 alpha_ik(파란선)는 Item-Item 관계를 모델링하는데 사용되나,

유저 u가 주어졌을 때 item(i)와 item(k)의 가중치가 비대칭적인 문제가 있다.

-> 수식을 뜯어보면, item(i)는 1/(d_i + 1)의 가중치를 부여 받으나, item(k)는 1/sqrt(d_i+1)의 가중치를 부여받는다. 이로 인해 성능의 저하가 있을 수 있다.

한계점 2. Message Passging에서 다양한 유형의 관계를 재귀적으로 결합한다.

- 다양한 유형의 관계를 재귀적으로 결합하면서 GCN이 성공하였으나, 노이즈가 많거나, 불필요한 관계가 발생하는 부분때문에 학습 효율성에 큰 저하를 발생시킬 수 있다.(4.4절에서 다룸) -> it is also pointed at SimpleX

한계점 3. 레이어 수와 high-order signals의 관계를 살펴보면, Over Smoothing의 이슈가 발생함.

- OverSmoothing 이슈로 LightGCN에서도 3번째 레이어까지만 구성함. 동일한 Item을 갖고 있거나, 동일한 User를 갖고 있는 경우 Layer가 많이 쌓일 수록, 동일한 임베딩을 갖게 되게 된다. 아래 식에서 무한번의 Laplacian Smoothing을 할 경우 어떻게 수렴이 되는지 표현한 식으로 동일한 임베딩을 갖는것을 보여준다.

위와 같은 한계점 3가지 때문에, Layer를 통과하는게 명시적으로 필요한지 의문을 제기하고, UltraGCN을 제안한다.

3. UltraGCN

위의 한계점들 때문에, Layer를 통과하는 Explicit한 Learning말고, 궁극적으로 도달하고자 하는 Embedding으로 Mapping 하는 방법이 없을까?

3.1 User-Item Graph

무한개의 Layer를 통과한 유저의 임베딩은 아래와 같이 표현 할 수 있을 것이다.

이를 3번 식에 대입하여 풀이하면 9번식을 유도할 수 있다.

다른 말로 하면, 각각의 노드가 9번의 식을 만족하면 Message Passing이 수렴된 것으로 생각할 수 있다.

우리가 궁극적으로 훈련이 되면 좋겠는 방향은 특정 user embedding과 연관된 edge(item)들의 interaction이 최대는 방향으로 생각해 볼수도 있다.

이를 논문에서는 아래와 같이 표현하였으나

수도 코드로는 아래와 같이 간단하게 표현할 수 있다.(Score가 최대가 되는 방향으로 학습)

위의 수식은 코사인 유사도를 최대화 하는 것과 같은말임. Activation Function인 Sigmoid와 Negative Log likelihood로 표현하면 아래와 같다.

하지만 Loss C 만으로는 문제점이 있다. 2.2절에서 언급한 한계점 중 하나인 OverSmoothing문제를 해결하지 못한다.

위 Loss로 학습할 경우, User와 Item의 Embedding이 비슷한 Representation을 갖을 수 있다.

- LightGCN의 경우, OverSmoothing을 피하기 위해, Layer를 얕게 쌓는 방법을 취함.

OverSmoothing을 피하기 위해, Word2Vec에서 사용하는 Negative Sampling 방법을 차용하였다.

Positive Sample에 대해선 11번 식에서 설명하여 생략하고, NegSample에 대해서 설명하자면

User vector와 Neg Item Vector의 방향 벡터가 다르면 다를 수록 좋다.

따라서 Vector곱이 음수가 나오면 좋은데, 이를 Loss Function에 녹아내기 위해 -를 곱하여 표현하였다.

여기서 Beta_user_item  Term은 가중치로 볼 수 있다.

만약 한명의 유저가 많은 Item에 상호작용 하거나, or vise versa한 상황이라면 가중치가 작아야 하는데 이를 Beta가 역할을 수행한다고 보면 된다.

다만, CF문제에서는 일반적으로 BPR Loss를 차용한다. 따라서 이 논문에서도 BPR Loss를 주 Loss Function으로 사용한다.

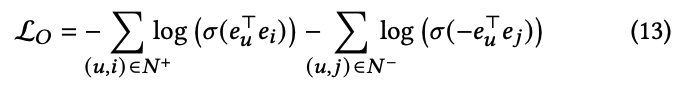
최종적인 Loss는 아래와 같다.

3.2 Item-Item Graph

5번 수식에서 볼 수 있듯 User-Item 관계 외에도 User-User, Item-Item도 GCN CF에서 크게 기여하는 부분이 있다. 그러나 기존 모델들은 User-Item관계와 같은 Layer와 Loss를 통해서 학습 된다. 이로 인해 가중치가 불균형하게 설정될 뿐만 아니라 다양한 관계에 있어 상대적인 중요도를 파악할 수 없다(2.2절 한계점1). 반면 이 연구에서는 명시적인 방법으로 학습하지 않기 때문에 보다 유연한 방법으로 관계별로 학습을 따로 진행할 수 있다.

아이템이 같이 발생한 메트릭스 G를 아래와 같은 방법으로 구한다.

9번 식처럼 유도를 진행하면 아래와 같이 유도할 수 있다.(수학적으로 어떻게 유도 하는지 모르겟다.)

방정식 12와 유사하게, 아이템-아이템 그래프에서 아이템 간의 관계를 학습하기 위한 제약 손실을 유도할 수 있으나 𝐺가 사용자-아이템 그래프의 Adjacency Matrix 𝐴와 비교하여 훨씬 밀도가 높기 때문에, 𝐺에 대한 제약 손실을 직접 최소화하는 것은 신뢰할 수 없거나 노이즈가 많은 아이템-아이템 쌍이 최적화 될 수 있어서 UltraGCN을 훈련하기 어려울 수 있다. 이는 또한 2.2절에서 설명한 기존 GCN 기반 모델의 제한 사항 II와 유사하다. 그러나 UltraGCN의 유연한 설계로 해결이 가능하다.

위에서 나온 W는 아이템 i와 j의 coefficient로 생각할 수 있는데, 간단하게 말하자면 아이템 i와 j의 관계 즉 얼마나 가까운지로 말할 수 있다. 따라서 아이템i 와 동시에 발생한 아이템 j들에 대해서, W기준으로 소팅을하고, 상관성이 가장 높은 k개의 item들을 선택한다.

Item-Item에 대한 Loss는 (17)과 같다. 유저 u와 연관된 Positive Item들 중, w가 높은 k개의 아이템을 선별한다. 유저 u와 아이템들간의  상관성을 구한뒤 Negative Log를 구하는게 Loss Function이다. 여기서 w는 각각의 유저 아이템 쌍의 가중치 역할을 한다.

UltraGCN의 최종적인 Loss는 (18)과 같으며, Lo(BPR), Lc(유저-아이템), Li(아이템-아이템)을 조합한 Loss이다.

3.3 정리

1. UltraGCN에서 엣지에 할당된 가중치 𝛽𝑖,𝑗 및 𝜔𝑖,𝑗는 CF에서 더 합리적이고 해석 가능하여 사용자-아이템 및 아이템-아이템 관계를 더 잘 학습하는 데 도움이 된다.

2. 명시적인 메시지 전달 없이도(Layer를 통과하지 않고도) U잘 작동하며, UltraGCN은 유연성을 가지고 있다. 또한, 모든 이웃 쌍에서 동일하게 학습하는 대신 Section 3.2에서처럼 유용한 훈련 쌍을 선택할 수 있으며 노이즈 데이터를 넣는 것보다 더 좋은 결과를 보여준다.

3. UltraGCN은 다양한 유형의 관계로 다중 작업 학습 방식으로 훈련되지만, (L𝐶, L𝐼, L𝑂)은 BinaryCrossEntropy형식과 비슷하여 훈련이 용이하며 빠르게 수렴한다.

4. UltraGCN의 설계는 유연하다. 𝛾를 0으로 설정하면 BPR을 사용 안하게 되며 (UltraGCN Base) 사용자-아이템 그래프에서만 학습한다.

UltraGCN에 User-User 관계를 모델링 하지 않는다. 주로 User의 특성이 아이템의 특성보다 훨씬 더 다양하기 때문이다. 우리는 User-User 공존 그래프에서 User-User 관계를 캡처하는 것이 어렵다는 것을 발견함. 뒤에서 User-User 공존 그래프에서의 학습이 UltraGCN에 현저한 개선을 가져오지 않는다는 것을 경험적으로 보여준다. 반면, 기존의 GCN 기반 CF 모델은 User-Item 그래프에서 모든 관계를 구별하지 않고 학습하기 때문에(즉, Limitation II), 성능 저하를 겪을 가능성이 있다. User-User 관계는 소셜 네트워크 그래프에서 더 잘 모델링 될 수 있으며, 이 부분은 향후 연구로 남겨둔다.

다른 모델과 UltraGCN의 관계성을 비교하는 섹션이 있으나 생략하겠다.

- Relation to MF

- Relation to Network Embedding Method

- Relation to One-Layer LightGCN

4. 실험

파라미터

- Learning Rate : 1e-4

- Batch_size : 1024

- NegSample : 300

- K : 10

- Embedding_dim : 64

- 𝜆 : [0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4]

- 𝛾 : [0.1, 0.5, 1.0, 1.5, 2.0, 2.5, 3, 3.5]

주의 : 본 게시글은 저자가 Recap용으로 작성하는 글로서 명확하지 않은 정의와 모호한 설명이 있을 수 있음.

논문 요약

1. CF는 (1)상호작용 인코더, (2)손실함수, (3)네거티브 샘플링 세가지로 구성이 되어 있으며, (2),(3)에 대한 연구는 진행 되지 않아 본 연구에서 심도있게 연구를 진행함.
2. 손실함수로 Cosine Contrastive Loss를 제안
3. SimpleX라는 간단한 아키텍쳐를 설계
-> LightGCN대비 NDCG@20에서 최대 48.5%의 성능을 개선

1. 개론

  CF 모델의 학습과정은 (1) 인코더, (2)손실함수, (3)네거티브 샘플링 세가지 구성으로 이루어 진다. 대부분의 연구는 User Item 관계를 인 코더를 복잡하게 설계하며 해결 하는데 초점을 맞춘다. 예를들어 MLP, AutoEncoder, AttentionNetwork, Transformer, GNN등 다양한 연구 분야들이 CF를 풀기위해 연구되어 왔다. 

  반면, 손실함수 및 네거티브샘플링에 대한 연구는 거의 이루어지지 않았다. 손실함수에 있어서 BPR, CrossEntropy, SoftmaxCrossEntropy, Pairwise HingeLoss, MeanSquareError등 연구되어 왔으나, 손실함수들간의 비교를 하는 연구는 부족했다.

이 논문에서는 BPR & 적은 네거티브샘플링을 한 조합에서 결과가 좋지 않다는 것을 발견하였고, 적절한 손실함수 및 네거티브샘플링을 선택하는게 중요하다는 것을 발견하였다.

  SimpleX를 단순성에 집중하여 YoutubeNet, ACF등에서 아이디어를 차용하여 설계를 하였다. SimpleX는 행렬 인수분해, 유저 행동 모델링으로 구성되었으며, 유저 행동 모델링에서 과거 사용자의 선호 벡터들을 취합 및 가중합하고, 유저의 데이터와 융합한다. 매우 단순해 보이지만, 높은 효율성으로 인해 산업 응용 분야에 큰 잠재력을 가지고 있을 것이라 생각된다.

2. 대표적인 연구들 돞아보기 ( 생략 가능 )

2.1 MF기반 알고리즘 : User-Item 상호작용 행렬을 두개의 저차원 잠재 행렬로 분해

두 개의 저차원 잠재 행렬로 분해하여 User, Item을 표현한다.

- GRMF : 라플라시안 정규화 기법을 추가

- Hop-Rec : MF와 Graph기반 모델을 통합한 효율적인 방법론 제안

2.2. AutoEncoder-Based 방법론

AutoEncoder 아키텍쳐를 활용해, User, Item의 Embedding을 학습한다. 이 방법론은 Inductive( 한 User 그룹으로부터 학습하면서 동일한 후보 항목을 가진 다른 User그룹에 대한 추천을 수행)하는데 적합한 방법론이다.

대표적인 연구로는 VAE를 적용한 MultVAE, MacridVAE, EASER등이 있다.

2.3. GNN 방법론

최근 연구에서는 GNN 기반의 CF모델의 연구가 활발히 진행되고 있다. 대표적인 연구로는

- GraphSage

- PinSage : GraphSage개선한 아키텍쳐 제안

- NGCF : 임베딩 propagation을 사용하여 CF를 고차원 관점에서 인코딩하는 방법론

- LightGCN : 비선형과, 선형변환을 제거

- BGCF : 유저-아이템 그래프의 불확실성을 모델링

- DGCF : 유저-아이템 그래프의 의도 분포를 모델링

(NIA-GCN, NGAT4Rec, SGL_ED, DHCF, LCFN 등 많은 연구가 존재)

3. 본 연구

3.1 손실함수

이 논문의 주된 연구인 Loss에 대해서 먼저 살펴보자. 이 논문은 제안한 CosineContrastiveLoss와 ( BPR / PairwiseHingeLoss, BinaryCrossEntropy, SoftmaxCrossEntropy, MeanSquareError ) 에 대해서 실험을 진행하였다.

간략하게 설명을 하자면 빨간 색은 Positive Sample에 대한 부분이며, 파란 부분은 Negative Sample에 대한 Loss 부분이다. Margin을 NegativeSample에 주면서, 노이즈에 로버스트하게 학습이 되도록 설계를 한 것으로 보인다.

- 왜 CosineSim을 사용했을까? -> 연구에서는 유저/아이템 Representation의 크기가 인기도에 따라 크게 편향될 수 있기 때문에 사용했다고 밝히고 있다.

- Neg Sample수가 많아지면, 일반적으로 중복되는 정보이며 정보가가 없는 샘플들이 존재한다. BPR과 같은 손실함수에서는 NegSample을 Positive와 동등하게 처리하고 있다. 따라서 모델이 학습할 때 불필요한 노이즈 데이터에 압도되어 모델 성능이 크게 저하되고 수렴 속도도 느려질 수 있다. 본 Loss에서는 m 보다 큰 코사인 유사도를 갖는 하드한 샘플들에 대해서만 학습을 진행할 것이므로 훈련이 더 잘 진행된다.

- 위에 보이는 Loss에서 빨간 부분과 파란 부분을 동일한 가중치로 학습을 진행할경우, 파란부분의 데이터 셋이 훨씬 많기에 모델 성능이 저하될 수 있는 사실을 발견하였다. 

3.2 아키텍처

모델의 구조는 생각보다 간단하다(YouTubeNet, ACF, PinSage에서 따왔음을 밝혔다).

이 논문의 주 기여점은 LossFunction에서 발생하기 때문인 것 같다.

모델은 크게 [유저의 정보, 유저와 관련된 아이템의 정보, 그리고 후보가 되는 정보] 세가지 구조로 되어 있다. 유저의 임베딩 벡터와, 그 유저와 연관 있는 아이템들의 Aggregate된 정보들의 가중합을 진행하고, 후보가 될 수 있는 아이템들관의 관계성으로 추천을 진행한다. 

자, 하나씩 뜯어보자

Aggregate에 해당하는 부분을 먼저 살펴보자. (H_u : User U에 속하는 K개의 상호작용한 Item들)

Pu인 User한명에 대하여 가정하고 살펴 보자. 한 User에서 뽑힐 수 있는 Maximum한 아이템 데이터 셋은 K개다. 

위 그림에서 2개의 Interact가 있고, K=3이라고 가정하자. 3개까지 Item을 채워야 하니, 임의 벡터 I_3를 추가하되, Indicator를 통해 0,1로 가중을 주어 정보를 추가하거나 제거한다. (위 그림에서는 편의상 가중치인 alpha를 제외 하였음)

위 논문에서 제안한 alpha는 두가지 방법이 있다. 1) 가중평균, 2) 어텐션. 

가중평균은 User U가 갖고 있는 Item의 수로 나누면 되는것이며. Attention은 우리가 일반적으로 알고 있는 Attention 구조와 동일하다.

Aggregate된 정보와 User의 정보를 합치는 과정이 필요한 이유를 연구에서는 이렇게 밝히고 있다. Aggregate정보와, User의 정보는 다른 latent Space에 있기에 두 정보를 섞는 과정이 필요함을 언급하였다. (여기서 V는 Learnable Matrix)

이렇게 섞인 User정보를, 다양한 Item Vector들과 비교하며 유사성을 판단한다. 간략하게 Matrix들로 표현하자면 아래와 같다.

4. 연구 결과

1) 손실 함수와 음의 샘플링 비율의 영향 연구

2) 세 가지 주요 데이터 세트에서 기존 모델과 성능 비교

3) 다른 모델에 CCL 통합

4) 매개 변수 분석 및 효율성 평가 수행

5) 다른 데이터 세트에서 SimpleX 추가 검증

• 11개의 데이터 셋.
• NegSampling수를 1~2000까지 실험(대부분 100,500,1000에서 좋은 결과를 얻음).
• 마진(m)은  0.1 간격으로 0∼1 사이에서 실험(Amazon-Books, Yelp2018 및 Gowalla에서는 각각 0.4, 0.9,0.9에서 좋은 성능)
• 비교 모델과 동일한 임베딩 크기(예: LightGCN에서는 64, LCFN에서는 128)를 사용

4.1 손실 함수 실험

기존 연구들은 CF 모델 학습에서 손실 함수의 중요성은 간과하고 있다. 간단한 모델이 더 잘 설명하는 경향이 있기 때문에 가장 단순한 기본 CF 모델 중 하나인 MF를 백본으로 실험을 수행한다. 

• 1) CCL은 세 가지 데이터 세트 모두에서 일관되게 최고의 성능을 달성
• 2) BPR은 Gowalla에서만 강력한 것으로 나타났으며, Amazon-Books와 Yelp2018 모두에서 성능이 좋지 않음.

왜 CLL이 좋은가?

• 구별하기 어려운 하드 네거티브 샘플을 필터링할 수 있다. 마진(m)을 사용하여 노이즈가 있는 데이터 셋들은 Loss에서 계산되지 않는다. 마진보다 큰 하드 네거티브 샘플에 대해서만 Loss에 기여하여, 하드 네거티브와, 파지티브 데이터 간의 구별하는데 중점을 두고 있다.
• PHL도 거리 개념을 사용하나, 음성과 양성 사이의 상대적 거리를 사용하기 때문에 하드 네거티브와 양성간의 차이가 얼마 차이가 나지 않더라도, 하드 네거티브의 Loss가 반영되지 않을 수 있다. 예) 하드네거티브의 예측값이 0.8, 양성이 0.9일 경우 둘 간의 거리가 가깝기에 하드 네거티브가 Loss에 영향을 주지 못한다.

4.2 네거티브 샘플링의 비율

• NegSample의 수의 중요성 : 일반적으로 일정 범위에서 NegSample이 증가하면 성능이 향상된다. 
• CLL의 우수성
• PHL, MSE, BPR의 성능은 음성 샘플 수가 50개 까지 성능향상이 있다. 반면, CCL, BCE, SCE는 음성 샘플 수가 1000개까지 증가해도 성능 향상이 있다.

4.3 SOTA모델들과 비교

MF와 CCL로스를 사용한 모델이 과거 모델들의 성능들을 앞선다.

4.4 다른 SOTA모델 + CCL 조합

• YoutubeNet, LightGCN + CCL 조합을 실험해본 결과, MF-CCL과 비슷한 성능을 보임을 확인함. 하지만, MF-CCL많큼의 성능 향상이 발생하진 않았다.
• 결론1 : LightGCN과 같은 인코더는 biased CF 데이터를 학습하는데 영향력을 끼치기에 손실 함수가 미치는 영향이 상대적으로 작아 보인다.
• 결론 2 : MF, YouTubeNet, LightGCN을 사용한 실험을 통해 손실 함수가 CF 모델에서 큰 병목 현상이라는 것을 입증하고 강조한다.

4.5 SimpleX의 파라미터 분석

• 논문에서 밝히길, avg_pooling, self_attn, user_attn, 모두 비슷한 성능을 보인다고 하였으며
• g=0.5 Amazon-Books의 다른 두 설정에 비해 더 높은 성능을 보이며, 이는 사용자 임베딩과 사용자 행동 집계를 융합하는 것이 중요하다는 것을 보여준다
• PosSample, NegSampe 비율을 조정하는 음의 가중치 w는 모델 성능에 매우 중요한 요소이며, 일반적으로 PosSample과 NegSample 차이가 너무 작거나(w = 1) 너무 크면(w = 1000) 성능 저하로 이어진다.

4.6 훈련 시간(효율성)

최종 훈련시간을 살펴보면, SimpleX의 훈련시간은 타 모델의 훈련시간을 압도한다...

4.7. 추가적인 실험

주의 : 본 게시글은 저자가 Recap용으로 작성하는 글로서 명확하지 않은 정의와 모호한 설명이 있을 수 있음.

요약 : 
1. Collaborative Filtering문제에서 Graph는 획기적인 성능향상을 갖고 왔으나, 이유는 뚜렷하지 않음(실험적인 증거만 있음)
-> 본 연구에서 Graph이론이 왜 잘 작동을 하는지 씹고 뜯고 맛보고 할 것임. (Activation Function, Feature Transformation 관점)
2. 1에서 밝힌 실험 결과로 새로운 아키텍쳐인 LightGCN을 제안.

1. 개론

- CF(Collaborative Filtering)를 통한 학습

   Transaction데이터를 통해 User와 Item의 임베딩을 학습하여 예측을 수행함.

- GCN구조를 CF문제를 풀기위해 응용하면서 갖고오는 시사점

   User와 여러 Item들 간의 관계성을 Embedding하기 위해 GCN구조를 NGCF논문에서 제안하였으며, SOTA를 달성함.

   다만, GCN구조를 추천시스템에 무작정 갖고 오면서, 완벽한 Fit을 갖추지는 못하였다고 주장함.

- GCN에서는 노드가 풍부한 속성을 입력 특성을 갖고, 노드 분류를 위해 제안되었으나,

   CF에서는 [0,1]로 이루어진 Transaction으로 복잡한 비선형성과, 변환을 통한 Embedding을 학습하는 것은 어렵다고 말한다.

NGCF에서 Activation, Transformation을 제거하여 더 높은 성능을 이끌어냄.

2. NGCF 돞아보기

논문에서 위와같은 복잡해 보이는 수식들이 나오나.

쫄필요 없다. NGCF논문에서 이미 다루었던 수식을 그대로 재탕한 것 뿐이다.

NGCF논문을 다루었으니 여기부터 둘러보고 오시는걸 추천한다.

https://jihoonjung.tistory.com/63

다시 돌아가서, 논문의 저자는 공평한 실험을 위해 기존 NGCF구조를 살짝 변경하였다.

기존의 NGCF논문은 Layer를 통과한 Embedding을 concat했다면, LightGCN저자는 Embedding을 통과한 벡터들의 합으로 변형하였다. 

# 기존 NGCF
torch.concat([layer1, layer2, layer3, ...])

# LightGCN
torch.sum([layer1, layer2, layer3, ...])

NGCF로 실행한 실험 방법 :

• NGCF-f : [NGCF Node 학습 방법 수식] 그림에 있는 W1, W2 제거 -> Transformation 제거
• NGCF-n : Activation Funtion 제거
• NGCF-fn : Activation, Transformation모두 제거

Activation Funtion만 제거(NGCF-n) : 성능이 안좋아짐

Transsformation제거(NGCF-F) : 성능이 기존과 비슷하거나 좀 더 좋음.

두개 모두 제거할 경우(NGCF-fn) : 성능이 매우 좋아짐.

이러한 증거를 통해 NGCF의 성능 저하는 과적합이 아니라 훈련 난이도에서 기인한다는 결론을 도출할 수 있다. 이론적으로는 NGCF가 NGCF-f보다 더 높은 Representation을 갖어야 하나 실제로는 NGCF가 NGCF-f보다 Traning Loss가 더 크고 성능이 안좋음.(데이터 특성과 복잠성을 따져보지 않고 Parameter만 많다고 최고는 아니다.)

3. LightGCN

k번째 layer에 속한 user노드는 위와같은 방법으로 k+1 embedding된다.  user u 와 관련이 있는 k번째 item들의 embedding들을 불러오고 Aggregate한다. 여기서 aggregate은 LSTM, WeightSum, bilinear등의 방법으로 정보를 합쳤었는데, 모두 Trainablegks Weight들이었다. 저자는 Agg부분을 간소화 하는 방법을 아래와 같이 제안함.

e_u 에 대해서만 설명을 하자면, k+1번째 user의 임베딩 : user와 연관이 있는 item들의 k번째 임배딩들의 normalized sum으로 볼 수 있다. -> 저자의 주장대로 Trainable Weight이 없음.

여기서 유일하게 Trainable Weight은 0번째 임베딩이다. 

각 Layer마다 계산된 Embedding들의 가중합을 진행하는데, 저자의 연구에서는 Uniformly하게 가중치를 주는 것이 가장 좋은 성능을 보였다고 한다.(또한 Weight을 Trainable하게 두지 않는 것도 이유였음.)

가중합을 하는 이유

• 레이어 수가 증가하며, 맨끝에 있는 embedding은 너무 광범위한 특성을 갖고 있음(over-smoothed) 따라서 맨 마지막 레이어를 사용하는 것은 문제가 있음.
• 각 레이어는 서로 다른 의미를 내포하고 있음. 예) 첫번째 레이어는 사용자와 직접적으로 연관성이 있는 아이템들의 정보들이 섞여 있으며, 두번째는 사용자 - 아이템 -사용자까지의 정보를 포함하고 있다. 즉 레이어가 쌓일수록 High Level View를 갖게 된다.

3.1 Data 준비하기

A라고 표시된 Laplacian Matrix을 준비한다. 위 내용은 https://jihoonjung.tistory.com/63 여기서 다루었음.

E = concat([user, item]) 을 한 메트릭스이다. 여기서 user, item은 임베딩된 vector이다.

다만 달라진 점은, self-connection을 제거하였다. ( A + I 에서 I 부분 제거) wher ( I = identical Matrix )

그 근거로는 weight sum of diffent layers하므로 불필요하다고 말하고 있다.

3.2 LightGCN 코딩

# LightGCN에서 유일하게 Trainable한 0번째 Embedding을 정의한다.
def init_embedding(self):
    self.E0 = nn.Embedding(self.n_users + self.n_items, self.latent_dim)
    nn.init.xavier_uniform_(self.E0.weight)
    self.E0.weight = nn.Parameter(self.E0.weight)
    
# Layer를 통과하며 나온 Embedding결과물을 Concat한다.
def forward_layers(self):
    current_embedding = self.E0.weight
    all_embeddings = [current_embedding]

    for _ in range(self.n_layers):
    	# layer하나를 통과하며, 현 시점과 관련된 item(혹은 User)정보를 불러와 Sum한다. -> Msg and Aggregate
        current_embedding = torch.sparse.mm(self.laplacian_matrix, current_embedding)
        all_layer_embedding.append(current_embedding)

    all_layer_embedding = torch.stack(all_layer_embedding)
	# 각 레이어에서 나온 결과물들을 alpha로 가중합을 한다. -> 본 연구에서는 Uniform한 합이 가장 좋은 결과물이 도출되어 mean을 사용해 가중합 함.
	mean_layer_embedding = torch.mean(all_layer_embedding, axis = 0)

    final_user_Embed, final_item_Embed = torch.split(mean_layer_embedding, [n_users, n_items])
    initial_user_Embed, initial_item_Embed = torch.split(self.E0.weight, [n_users, n_items])

    return final_user_Embed, final_item_Embed, initial_user_Embed, initial_item_Embed

3.3 Loss Function : BPR Loss

NGCF와 동일한 Loss Function인 BPR Loss를 사용함.

def bpr_loss(users, users_emb, pos_emb, neg_emb, userEmb0,  posEmb0, negEmb0):
  
    reg_loss = (1/2)*(userEmb0.norm().pow(2) + 
                    posEmb0.norm().pow(2)  +
                    negEmb0.norm().pow(2))/float(len(users))
    pos_scores = torch.mul(users_emb, pos_emb)
    pos_scores = torch.sum(pos_scores, dim=1)
    neg_scores = torch.mul(users_emb, neg_emb)
    neg_scores = torch.sum(neg_scores, dim=1)
        
    loss = torch.mean(torch.nn.functional.softplus(neg_scores - pos_scores))
        
    return loss, reg_loss

4. 실험결과

4.1. NGCF VS LightGCN

• 레이어 수를 증가 시키면 일반적으로 성능이 향상하나, 성능향상 폭은 감소한다

4.2. Comparing with other Models

다른 모델들과 비교를 하고, 모든 데이터 셋 및 모델 보다 더 좋은 성능을 보인다.

(Mult-VAE는 나머지 모델들과 비교했을때 가장 성능이 좋긴함)

4.3. Effectiveness : Combinations of Layers

가장 끝 layer에 나온 Embedding을 사용하지 않고, Layer마다 나온 결과물을 왜 Combination을 해야하는지 ablation Study에서 논의한다.

Figure 4.
Layer의 최종 아웃풋을 기반으로 성능을 측정했을 경우, Gowalla의 경우 모든 Layer에서 Combination을 이기지 못하는 모습을 보인다. 반면 Amazon은 4번째 Layer이후 Combination보다 낮아진다.
-> 단일 Layer를 사용할 경우 Layer가 쌓일수록 OverSmoothing이 적둉이되어 성능 하락이 이루어 진다.
-> 반면 LightGCN의 경우 Layer가 쌓여도 증가한다.

Figure 5.
- 일반적으로 가장 좋은 설정은 양쪽 모두 sqrt 정규화를 사용하는 것(즉, 현재 LightGCN의 설계). 어느 한 쪽을 제거하면 성능이 크게 떨어짐
- 두 번째로 좋은 세팅은 왼쪽에만 L1 노멀라이제이션을 사용하는 것(즉, LightGCN-L1-L). 이는 인접 행렬을 차수만큼 확률 행렬로 정규화하는 것과 같음.
- 양쪽을 대칭으로 정규화하면 sqrt 정규화에는 도움이 되지만 L1 정규화의 성능이 저하됨.

주의 : 본 게시글은 저자가 Recap용으로 작성하는 글로서 명확하지 않은 정의와 모호한 설명이 있을 수 있음.

서론
- 기존 문제의 단점 : 유저, 아이템의 데이터적 특성을 갖고 임베딩을 할 경우 CF에선 충분한 임베딩을 생성하기 힘들다.
                               유저를 대표할만한 latent를 뽑기 힘든데, 이유로는 유저, 아이템 상호작용을 잡아내는 인코딩이 없기 때문이다.
(The key reason is that the embedding function lacks an explicit encoding of the crucial collaborative signal, which is latent in user-item interactions to reveal the behavioral similarity between users (or items))

- 본 연구 : high-order 정보를 연결하는 모델링을 하겠다.(By Graph)
1. CF에서 발생한 Transaction을 사용하는게 매우 중요하다.
2. High-order connectivities를 학습할 수 있는, NGCF모델을 제안한다.
3. 3백만 데이터 셋에 대한 검증을 완료

1. Embedding Layer

import torch.nn as nn
import torch

# 유저와, 아이템을 각각 d차원의 벡터로 맵핑
embedding_dict = nn.ParameterDict({
    'user_emb': nn.Parameter(initializer(torch.empty(self.n_user,self.emb_size))),
    'item_emb': nn.Parameter(initializer(torch.empty(self.n_item,self.emb_size)))
})

# 위 코드 혹은 아래 코드 가능
embedding = nn.Parameter(nn.Embedding(self.n_user + self.n_item, self.emb_size))

위 임베딩들은 Item-User관계를 보며 학습 될 것임.

1. Data 준비

논문에서 R이라는 것이 정의가 되며 [N*M]의 차원을 갖고 있고, 0과 1로 채워진 메트릭스이다. 여기서 1은 implicit 혹은 explicit 한 정보를 담고 있으며, 0은 transaction이 발생하지 않은 것으로 생각하면 될 것 같다.

그림으로 표현하면 아래와 같은 메트릭스로 표현할 수 있다.

adj_mat = sp.dok_matrix((self.n_users + self.n_items, 
                         self.n_users + self.n_items), dtype=np.float32)
adj_mat = adj_mat.tolil()
R = self.R.tolil()

adj_mat[:self.n_users, self.n_users:] = R
adj_mat[self.n_users:, :self.n_users] = R.T

Laplacian에서 D**(-1/2)AD**(-1/2)로 표현을 하였는데, 보기에 복잡해 보이나, 실상은 간단하다.  User-n과 Item-L의 row와 column에서 갖고 있는 1의 갯수를 (-1/2)한것이다. 

# 각 Row별 몇개의 Transaction이 발생했는지 카운팅
rowsum = np.array(adj.sum(1))

# x**(-1/2) 변환
d_inv_sqrt = np.power(rowsum, -0.5).flatten()

# Transaction이 없으면 inf가 발생하여 0으로 변환
d_inv_sqrt[np.isinf(d_inv_sqrt)] = 0.

# (n+m)*(n+m) 메트릭으로 변환하는데, d_inv_sqrt값이 대각 행렬로.
d_mat_inv_sqrt = sp.diags(d_inv_sqrt)

bi_lap = d_mat_inv_sqrt.dot(adj).dot(d_mat_inv_sqrt)

Laplacian을 살펴보면, 핑스색 부분이 중복 되는 것을 볼 수 있다. Normalize한 R 매트릭스를 시점 관점에서(user관점에서, Item관점에서) Transpose를 하면 되는거 아닌가란 생각을 할 수 있는데 -> 맞다 그렇게 생각해도 되나, 계산상의 편의를 위해 Laplacian을 구한것이다.

자 데이터 셋은 이렇게 준비가 완료 되었다. 이제 아키텍쳐를 살펴보자

2. 아키텍쳐

이 논문 Contribution중 하나인 High-order propagation을 살펴보자. 일반적으로 Graph에서 많이 나오는 단어들은 Messaging, Aggregation이라는 단어들이 존재한다. Messaging은 Transaction이 발생한 구간들의 정보들을 하나의 노드들로 모으는 것을 의미하며, Aggregation 은 이렇게 모인 메시징을 모은다고 생각하면 편하다.

레이어 두개가 통과되면, 위 user는 item 과 연결된 user들의 정보들도 섞이게 된다.

Mu<-i 는 아래와 같이 구현 할 수 있다.

# A_hat = laplacian matrix [user+item, user+item]
# ego_embeddings  [user+item, dim]
# 첫번째 텀. W_1*e_i를 진행한다. Every Node에서 진행을 한다(Not using For loop. Use effiency of Matrix)
side_embeddings = torch.sparse.mm(A_hat, ego_embeddings)   # -> [user+item, dim]
sum_embeddings = torch.matmul(
    side_embeddings, 
    self.weight_dict['W_gc_%d' % k]
) + self.weight_dict['b_gc_%d' % k]

# 두번째 텀. W_2(e_i * e_u)를 진행한다.
bi_embeddings = torch.mul(ego_embeddings, side_embeddings)  # -> [user+item, dim]
bi_embeddings = torch.matmul(bi_embeddings, self.weight_dict['W_bi_%d' % k]) \
                                + self.weight_dict['b_bi_%d' % k]
                                
# 두개 텀을 합치기
ego_embeddings = nn.LeakyReLU(negative_slope=0.2)(sum_embeddings + bi_embeddings)

여기까지 따라오면 다 온것이다. 마지막 스텝만 하면 끝~

논문의 아키텍쳐를 보면, Every Layer마다 임베딩을 꺼내서 Concatenate을 하는 것을 볼 수 있다.

all_embeddings = []

for _ in layer:

	# 위 코드 블록에서 작성했던 코드들을 여기다가 작성
    #~~~~
    #~~~~
    #~~~~

    norm_embeddings = F.normalize(ego_embeddings, p=2, dim=1)
	# 나중에 모든 레이어마다 학습된 vector를 꺼내기 위해서, list에 저장
    all_embeddings += [norm_embeddings]
    
all_embeddings = torch.cat(all_embeddings, 1)
# 유저에 대한, 모든 layer에서 학습된 vector
u_g_embeddings = all_embeddings[:self.n_user, :]
# 아이템에 대한, 모든 layer에 학습된 vector
i_g_embeddings = all_embeddings[self.n_user:, :]

여기서 만들어진 u_g_embeddings와 i_g_embeddings를 바탕으로 Loss를 계산하고 학습한다.

3. Loss

논문에서 작성된 Loss는 위와 같이 생겼으며, BPR_LOSS라고 한다.

BPR_LOSS는 추후 다룰 SimpleX논문에서도 유의미하게 학습이 잘 된 Loss중 하나이며, 이것을 제대로 설명하는데는 시간이 필요하여 추후 정리해야겟다......

https://arxiv.org/abs/1905.08108