[논문리뷰] BitNet: Scaling Transformers for Large Language Models

 

MoRA논문을 읽다가, 양자화 관련 논문들이 궁금하여 리서치 중...

https://jihoonjung.tistory.com/94

[논문리뷰] The Era of 1-bit LLMs:All Large Language Models are in 1.58 Bits

https://jihoonjung.tistory.com/93

[논문리뷰] LLM.int8() : 8-bit Matrix Multiplication for Transformers at Scale

 

0 Abstract

• 확장 가능하고 안정적인 1-bit Transformer 아키텍처인 BitNet을 소개.
• 1-bit 가중치를 학습시키기 위해 nn.Linear 계층을 대체할 수 있는 BitLinear를 도입
• 언어 모델링에 대한 실험 결과, BitNet은 최신 8-bit 양자화 방법 및 FP16 Transformer 비교하여 메모리, 에너지 소비를 줄이면서 경쟁력 있는 성능을 달성
• BitNet은 full precision Transformer와 유사한 스케일링 법칙을 보임
  -> 효율성과 성능상의 이점을 유지, 더 큰 언어 모델로 효과적으로 확장될 수 있음을 시사

 

 

1 Introduction

기존 주 연구 대상 : 사전 학습 모델 -> 양자화  (사후 학습)

• 학습 파이프라인, 모델 재학습이 필요하지 않아 쉬움, 그러나 정밀도가 낮아질 때 최적화되지 않기 때문에 성능 하락

(quantization-aware training) 양자화 인식 학습

• 더 나은 정확도(사후학습 대비) : 처음부터 정밀도 감소를 고려하여 학습
• 지속적 학습, 미세 조정 가능
• 주요 과제 : 최적화(정밀도가 낮아질수록 모델의 수렴이 어렵다) -> 8bit, 4bit으로 내려갈 수록 어렵다.
• 스케일 법칙 따르는지 여부는 알 수 없음

본 연구 :

• 이진화(즉, 1-bit)에 주목
• 1-bit LLM 을 위한 양자화 인식 학습을 처음으로 조사
• 대규모 언어 모델용 1-bit Transformer 아키텍처인 BitNet을 제안
• BitNet은 perplexity와 다운스트림 작업 정확도 측면에서 기경쟁력 있는 성능을 달성
• 메모리 사용량과 에너지 소비를 상당히 줄인다
• BitNet이 전체 정밀도 Transformer와 유사한 스케일링 법칙을 따른다는 것을 보여줌
  -> 훨씬 더 큰 언어 모델로 효과적으로 확장될 수 있음을 나타냅니다.

 

2 BitNet

• Transformer와 동일한 레이아웃을 사용
• 바닐라 Transformer와 비교하여 BitNet은 BitLinear(식 11 이진화)를 기존의 행렬 곱셈 대신 사용.
• 나머지 구성 요소는 고정밀도로 유지(실험에서는 8-bit를 사용) 이유 : 
  • 첫째, Residual Connection과 Layer Norm은 계산 비용
  • 둘째, QKV 변환의 계산 비용은 모델이 커질수록 Parametric projection(Linear를 의미하는 것 같음)에 비해 훨씬 작습음.
  • 셋째, 언어 모델이 샘플링을 수행하기 위해선 고정밀 확률을 사용해야 함.

2.1 BitLinear(figure 2)

이 부분은 Weight부분이다. Nothing to do with X Tensor. Figure2의 보라색 부분

• 모든 웨이트(W)에 대해 알파값을 빼 평균이 0이 되도록 변환하고, 이를 sign함수에 맵핑하여 (-1,1)로 맵핑.
  -> 가중치를 평균이 0이 되도록 변환(제한된 numeric 범위 내에서 용량을 높이기 위해)
  -> signum 함수를 사용 : 가중치를 +1 또는 -1로 변환.
  W : 웨이트
  alpha : 모든 웨이트의 합을, 웨이트의 갯수만큼 나눈 평균 값
• β : 실수 가중치와 이진화된 가중치 사이의 l2 오차를 줄이기 위한,스케일링 계수

 

이 부분은 X Tensor에 대한 부분(Input)

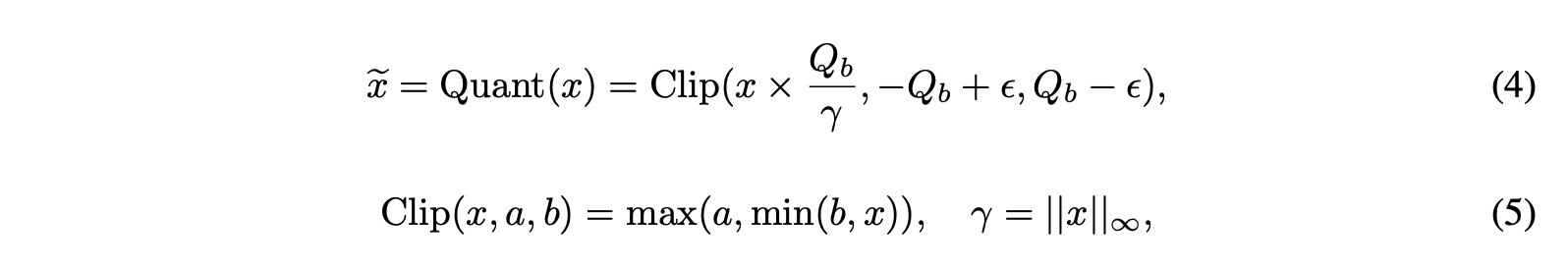
• Quantize Activations : b-bit 양자화. 입력 행렬의 절대 최대값으로 나누고 Q_b를 곱하여 활성화를 [-Q_b, Q_b] 범위로 스케일링(aka absmax - minmax scaling과 비슷하지만, 절대값을 하고난 스케일링 으로 생각) 
• Clip(x,a,b) : a<x<b가 되도록 하는 함수
• Quant(x) : [-Q_b, Q_b]범위가 되도록 함.
• 무한대 놈 : 텐서중 절대값 최대 값.

예시
Q_b = 127 (8비트 양자화) 
x = [0.1, -0.2, 0.3, -0.4]
# 맥스놈
γ = 0.4
# 스케일링 펙터
Q_b/γ = 127/0.4 ≈ 317.5
#스케일링 후 -> 모든 값이 [-127, 127] 사이에 있음.
x × (Q_b/γ) ≈ [31.75, -63.5, 95.25, -127]

 

ReLU와 같은 비선형 함수는 모든 값이 음수가 아닌 값이 되도록 입력의 최소값을 빼서 [0, Qb ] 범위로 스케일링한다 : 아래 식

(7) 식은 Figure 2에 왼쪽 그림에 곱(x)를 의미.

(8)(9)(10) 식에서는 Pre LayerNorm의 유익한 점에 대해서 설명하고 있음. PreLayerNorm을 하게되면, Var(y) = 1이 되고, 훈련의 안정성에 큰 이익이 있다고 함.

 

그래서 최종적으로 식을 정리하면 아래와 같이 된다.

 

Model parallelism with Group Quantization and Normalization

-> 생략

 

2.2 Model Training

 

Straight-through estimator : 미분, 역전파를 우회하기 위한 방법

• 역전파 중에 기울기를 근사화하기 위해 straight-through estimator 사용
• 이 방법은 역방향 전달 중에 Sign(식 2) 및 Clip(식 5) 함수와 같은 미분 불가능한 함수를 우회
  • 순전파 : 계값을 기준으로 0 또는 1로 이산화
  • 역전파 : 역전파에서는 이 이산화 과정을 무시하고, 원래의 연속적인 출력 값에 대한 그래디언트를 그대로 사용
    (ref : https://velog.io/@jk01019/straight-through-estimator-STE )
  • -> 순전파때 이산화 하기 전의 값을 Store한다는 말인가?
    몇몇 리서치를 해본 결과 답은 아래와 같다.
•  

# sign 함수일 경우
forward: y = sign(x)
backward: dy/dx = 1 if -1 <= x <= 1 else 0
'''
순전파 시에는 Sign 함수를 그대로 사용하여 y를 계산
역전파 시에는 Sign 함수를 identity 함수로 간주하고, x가 -1과 1 사이일 때만 기울기를 1로 설정하고 나머지 경우에는 0으로 설정
'''

# clip 함수일 경우
forward: y = clip(x, a, b)
backward: dy/dx = 1 if a <= x <= b else 0
'''
순전파 시에는 Clip 함수를 그대로 사용하여 y를 계산
역전파 시에는 x가 a와 b 사이일 때만 기울기를 1로 설정하고 나머지 경우에는 0으로 설정
'''

 

 

 

Mixed precision

• 낮은 정밀도(양자화) : 가중치, 활성화
• 높은 정밀도 : 기울기, 옵티마이저, latent weight
• 반반 : 잠재 가중치 - 순방향 전달 중에 이진화되며, 추론에서는 사용되지 않는다.
  • 잠재 가중치 : 잠재 가중치는 높은 정밀도(예: 32-bit 부동 소수점)로 유지
  • How do adam and training strategies help bnns optimization. (구체적인 내용은 이 논문 참고)

Large learning rate

• 잠재 가중치에는 작은 업데이트(small update)가 1-bit 가중치에서 차이를 만들지 않는다는 어려움이 있음.
• 이유 : 1-bit 가중치를 기반으로 -> 편향된 기울기와 업데이트가 발생
• 학습 초기에 더 심함.
• 해결책 : 학습률을 높이는 것, 실험 결과 BitNet은 수렴 측면에서 큰 학습률에서 좋으나, FP16 Transformer는 동일한 학습률로 학습하면 gradient explode함.

2.3 Computational Efficiency

에너지 소비량(전기) 낮았다.

 

 

3 Comparison with FP16 Transformers

3.1 Setup

• 125M부터 30B 까지 실험
• Sentencpiece 토크나이저를 사용
• 동일한 데이터셋과 설정으로 BitNet ,Transformer 모델 학습

3.2 Inference-Optimal Scaling Law
-> Introduction에 언급하였지만, 양자화 학습이 스케일 법칙 따르는지 여부는 알 수 없음, 이를 실험하는 부분

 

파라미터의 수에 따른 모델 성능 예측 가능 (Llama3 에서도 언급 되었음)

• Scaling laws for neural language models.(논문)

이진 Transformer의 스케일링 법칙을 연구

• 매개변수 수에 대한 BitNet과 FP16 Transformer 기준 모델의 스케일링 곡선 그림.
• 학습 토큰 수를 고정하고 모델 크기를 변경
• 그림 3은 BitNet의 손실 스케일링이 FP16 Transformer와 유사
• 모델 크기가 커질수록 BitNet과 FP16 Transformer 사이의 격차가 감소

 

3.3 Results on Downstream Tasks

 

3.4 Stability Test

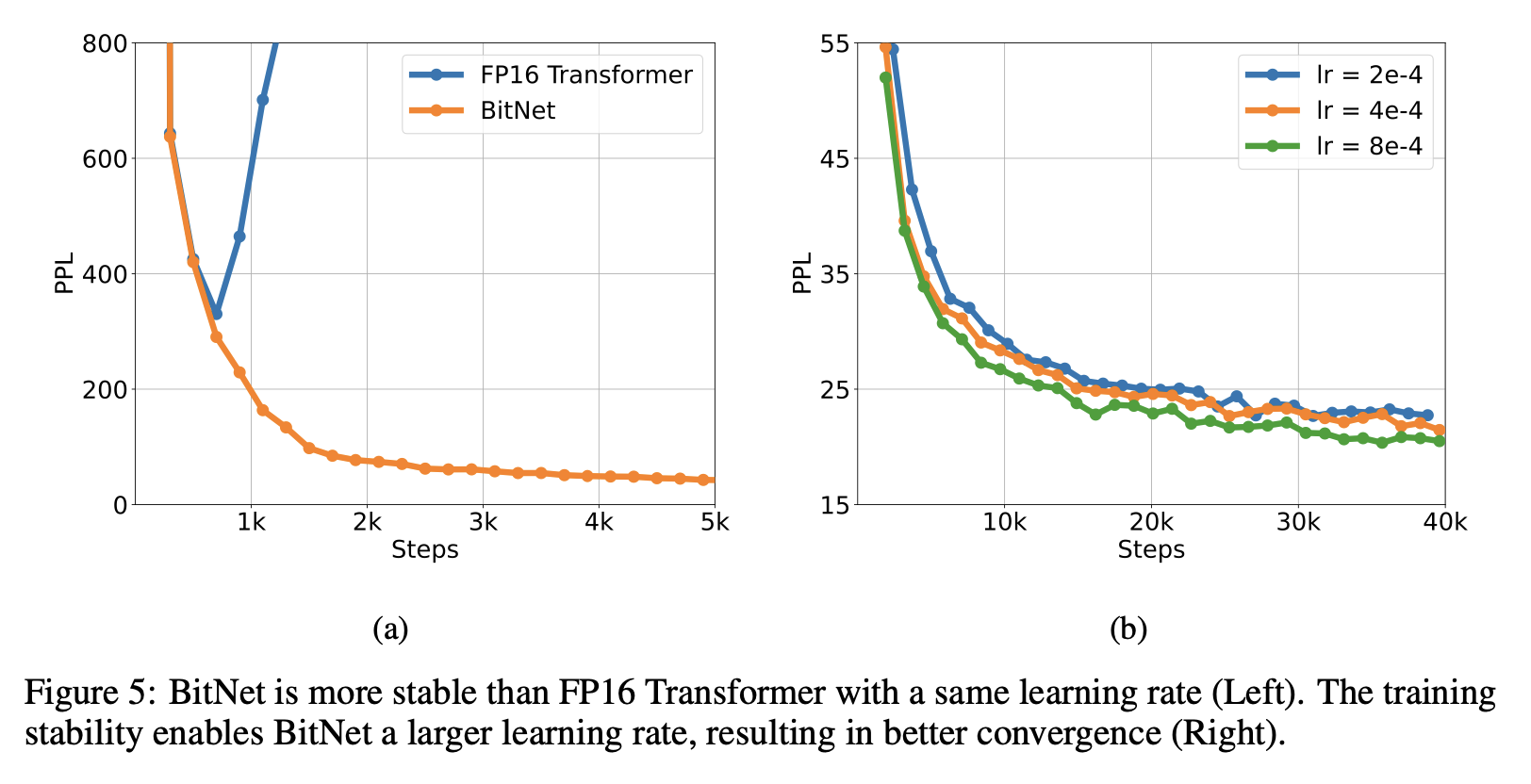
피크 학습률로 모델을 학습시켜 안정성 테스트를 수행

• BitNet은 큰 학습률로 수렴할 수 있는 반면 FP16 Transformer는 그렇지 않다
•  최적화에서의 이러한 장점은 더 큰 학습률로 학습할 수 있게 한다 -> 빠른 수렴
• (그림 5b) BitNet이 학습률 증가의 이점을 얻어 PPL 측면에서 더 나은 수렴을 달성할 수 있음.

4 Comparison with Post-training Quantization

최신 양자화 방법들과 비교

• FP16 Transformer 사후 양자화 : Absmax, SmoothQuant, GPTQ, QuIP
• Absmax, SmoothQuant : 가중치와 activation 모두를 양자화
• GPTQ, QuIP : weight 정밀도 줄임.

결과

• 6.7B의 모델에서 비교
• 16비트에서 1비트까지 다양한 가중치 비트 수준에 대해 평가
• perplexity가 포함
• 낮은 비트 수준에서 BitNet이 기준 방법과 비교하여 경쟁력 있는 성능 수준을 달성하는 데 효과적
• BitNet은 기준 방법과 비교하여 경쟁력 있는 성능을 달성함
• BitNet의 zero-shot 점수는 8비트 모델과 유사하지만 추론 비용은 훨씬 낮음
• 4비트 모델의 경우 가중치만 양자화하는 방법이 가중치와 활성화 모두를 양자화하는 방법보다 성능이 우수함
• 1비트 모델인 BitNet은 가중치와 활성화 양자화 방법과 가중치만 양자화하는 방법 모두 훨씬 더 나은 결과를 달성
• 더 낮은 비트 모델의 경우 BitNet은 모든 기준 모델보다 일관되게 우수한 점수를 보임
• 이는 사후 양자화 방법에 비해 양자화 인식 학습 접근 방식의 장점을 입증함
• 1.3B에서 6.7B로 모델 크기를 확장했을 때, BitNet의 장점이 다양한 규모에서 일관되게 나타남

5 Ablation Studies

-> BitNet의 구현에 absmax와 SubLN을 선택한 이유에 대해서 말하고 잇음