[논문리뷰 w/Code]NGCF : Neural Graph Collaborative Filtering 설명

주의 : 본 게시글은 저자가 Recap용으로 작성하는 글로서 명확하지 않은 정의와 모호한 설명이 있을 수 있음.

서론
- 기존 문제의 단점 : 유저, 아이템의 데이터적 특성을 갖고 임베딩을 할 경우 CF에선 충분한 임베딩을 생성하기 힘들다.
                               유저를 대표할만한 latent를 뽑기 힘든데, 이유로는 유저, 아이템 상호작용을 잡아내는 인코딩이 없기 때문이다.
(The key reason is that the embedding function lacks an explicit encoding of the crucial collaborative signal, which is latent in user-item interactions to reveal the behavioral similarity between users (or items))

- 본 연구 : high-order 정보를 연결하는 모델링을 하겠다.(By Graph)
1. CF에서 발생한 Transaction을 사용하는게 매우 중요하다.
2. High-order connectivities를 학습할 수 있는, NGCF모델을 제안한다.
3. 3백만 데이터 셋에 대한 검증을 완료

 

 

1. Embedding Layer

 

import torch.nn as nn
import torch

# 유저와, 아이템을 각각 d차원의 벡터로 맵핑
embedding_dict = nn.ParameterDict({
    'user_emb': nn.Parameter(initializer(torch.empty(self.n_user,self.emb_size))),
    'item_emb': nn.Parameter(initializer(torch.empty(self.n_item,self.emb_size)))
})

# 위 코드 혹은 아래 코드 가능
embedding = nn.Parameter(nn.Embedding(self.n_user + self.n_item, self.emb_size))

위 임베딩들은 Item-User관계를 보며 학습 될 것임.

 

 

 

1. Data 준비

 

논문에서 R이라는 것이 정의가 되며 [N*M]의 차원을 갖고 있고, 0과 1로 채워진 메트릭스이다. 여기서 1은 implicit 혹은 explicit 한 정보를 담고 있으며, 0은 transaction이 발생하지 않은 것으로 생각하면 될 것 같다.

그림으로 표현하면 아래와 같은 메트릭스로 표현할 수 있다.

adj_mat = sp.dok_matrix((self.n_users + self.n_items, 
                         self.n_users + self.n_items), dtype=np.float32)
adj_mat = adj_mat.tolil()
R = self.R.tolil()

adj_mat[:self.n_users, self.n_users:] = R
adj_mat[self.n_users:, :self.n_users] = R.T

 

Laplacian에서 D**(-1/2)AD**(-1/2)로 표현을 하였는데, 보기에 복잡해 보이나, 실상은 간단하다.  User-n과 Item-L의 row와 column에서 갖고 있는 1의 갯수를 (-1/2)한것이다. 

# 각 Row별 몇개의 Transaction이 발생했는지 카운팅
rowsum = np.array(adj.sum(1))

# x**(-1/2) 변환
d_inv_sqrt = np.power(rowsum, -0.5).flatten()

# Transaction이 없으면 inf가 발생하여 0으로 변환
d_inv_sqrt[np.isinf(d_inv_sqrt)] = 0.

# (n+m)*(n+m) 메트릭으로 변환하는데, d_inv_sqrt값이 대각 행렬로.
d_mat_inv_sqrt = sp.diags(d_inv_sqrt)

bi_lap = d_mat_inv_sqrt.dot(adj).dot(d_mat_inv_sqrt)

Laplacian을 살펴보면, 핑스색 부분이 중복 되는 것을 볼 수 있다. Normalize한 R 매트릭스를 시점 관점에서(user관점에서, Item관점에서) Transpose를 하면 되는거 아닌가란 생각을 할 수 있는데 -> 맞다 그렇게 생각해도 되나, 계산상의 편의를 위해 Laplacian을 구한것이다.

자 데이터 셋은 이렇게 준비가 완료 되었다. 이제 아키텍쳐를 살펴보자

 

 

2. 아키텍쳐

 

이 논문 Contribution중 하나인 High-order propagation을 살펴보자. 일반적으로 Graph에서 많이 나오는 단어들은 Messaging, Aggregation이라는 단어들이 존재한다. Messaging은 Transaction이 발생한 구간들의 정보들을 하나의 노드들로 모으는 것을 의미하며, Aggregation 은 이렇게 모인 메시징을 모은다고 생각하면 편하다.

레이어 두개가 통과되면, 위 user는 item 과 연결된 user들의 정보들도 섞이게 된다.

 

 

 

Mu<-i 는 아래와 같이 구현 할 수 있다.

# A_hat = laplacian matrix [user+item, user+item]
# ego_embeddings  [user+item, dim]
# 첫번째 텀. W_1*e_i를 진행한다. Every Node에서 진행을 한다(Not using For loop. Use effiency of Matrix)
side_embeddings = torch.sparse.mm(A_hat, ego_embeddings)   # -> [user+item, dim]
sum_embeddings = torch.matmul(
    side_embeddings, 
    self.weight_dict['W_gc_%d' % k]
) + self.weight_dict['b_gc_%d' % k]

# 두번째 텀. W_2(e_i * e_u)를 진행한다.
bi_embeddings = torch.mul(ego_embeddings, side_embeddings)  # -> [user+item, dim]
bi_embeddings = torch.matmul(bi_embeddings, self.weight_dict['W_bi_%d' % k]) \
                                + self.weight_dict['b_bi_%d' % k]
                                
# 두개 텀을 합치기
ego_embeddings = nn.LeakyReLU(negative_slope=0.2)(sum_embeddings + bi_embeddings)

 

 

 

 

여기까지 따라오면 다 온것이다. 마지막 스텝만 하면 끝~

 

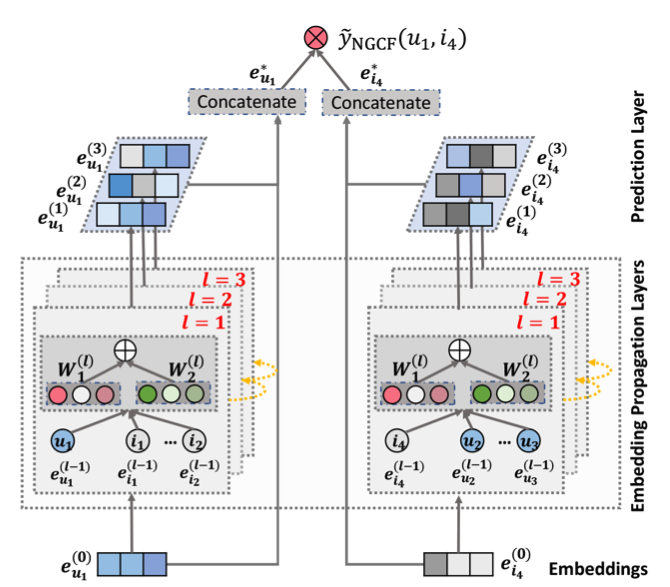
논문의 아키텍쳐를 보면, Every Layer마다 임베딩을 꺼내서 Concatenate을 하는 것을 볼 수 있다.

all_embeddings = []

for _ in layer:

	# 위 코드 블록에서 작성했던 코드들을 여기다가 작성
    #~~~~
    #~~~~
    #~~~~

    norm_embeddings = F.normalize(ego_embeddings, p=2, dim=1)
	# 나중에 모든 레이어마다 학습된 vector를 꺼내기 위해서, list에 저장
    all_embeddings += [norm_embeddings]
    
all_embeddings = torch.cat(all_embeddings, 1)
# 유저에 대한, 모든 layer에서 학습된 vector
u_g_embeddings = all_embeddings[:self.n_user, :]
# 아이템에 대한, 모든 layer에 학습된 vector
i_g_embeddings = all_embeddings[self.n_user:, :]

 

여기서 만들어진 u_g_embeddings와 i_g_embeddings를 바탕으로 Loss를 계산하고 학습한다.

 

3. Loss

 

논문에서 작성된 Loss는 위와 같이 생겼으며, BPR_LOSS라고 한다.

BPR_LOSS는 추후 다룰 SimpleX논문에서도 유의미하게 학습이 잘 된 Loss중 하나이며, 이것을 제대로 설명하는데는 시간이 필요하여 추후 정리해야겟다......

 

 

 

 

 

 

 

https://arxiv.org/abs/1905.08108

Neural Graph Collaborative Filtering