DeepLearing/NLP(Reasoning)
[논문리뷰] (25.03)L1: Controlling How Long A Reasoning Model ThinksWith Reinforcement Learning
notdecidedyet
2025. 4. 6. 22:20
이 논문은 성능을 많이 낮추지 않고도 토큰을 예산화 할 수 있다는 점에서는 신선하나,
다른 부분에서는 글쎄..? (작은 모델로 실험한 점, 훈련의 참신성은 좀 떨어짐...)
Abstract
- 문제:
- 추론 언어 모델은 "더 오래 생각하기"(더 긴 chain-of-thought)를 통해 성능을 향상시킬 수 있음
- 그러나 현재 모델들은 추론 길이를 제어할 수 없어 계산 자원 할당 최적화가 불가능
- 제안 방법:
- Length Controlled Policy Optimization (LCPO): 정확도와 사용자 지정 길이 제약 준수를 최적화하는 강화학습 방법
- L1 모델: LCPO로 훈련된 모델로 프롬프트에 주어진 길이 제약을 만족하는 출력 생성
- 주요 결과:
- 다양한 작업에서 계산 비용과 정확도 간 부드러운 교환이 가능
- 기존 길이 제어 방법인 S1보다 뛰어난 성능
- 예상치 못한 발견: 1.5B L1 모델이 동일한 추론 길이에서 GPT-4o를 능가
1. Introduction

- 배경 및 한계점: 추론 모델들은 더 길게 생각함으로써 복잡한 문제 해결 성능을 향상하나, 현 모델들은 추론 길이가 제어되지 않음. 복잡한 문제에서는 너무 일찍 멈추거나, 수만개의 토큰을 낭비하기도함. 이를 해결하기 위해 s1이라는 연구가 있었으나, 특수 토큰을 사용해 길이를 제어하는 것은 성능에 안좋은 영향이 있었음(figure 1).
- 이 연구의 제안: LCPO:
- 두 가지 목표를 만족시키도록 모델 훈련: 최종 출력의 정확성, 프롬프트에 지정된 길이 제약 충족
- 두 가지 실용적 제약 조건:
- LCPO-Exact: 생성된 추론이 목표 길이와 정확히 일치해야 함
- LCPO-Max: 출력이 목표 길이보다 길지 않아야 함
- L1 모델의 특징:
- 파인튜닝: Qwen-Distilled-R1-1.5B 기반 1.5B 파라미터 모델을 파인튜닝함.
-> 토큰을 길게 혹은 짧게 생성하여, 성능을 정밀하게 관리할 수 있음.
- 파인튜닝: Qwen-Distilled-R1-1.5B 기반 1.5B 파라미터 모델을 파인튜닝함.
- 주요 발견 및 기여:
- 학습 분포를 벗어난 작업(논리적 추론, MMLU 등)에도 효과적으로 일반화
- "긴-CoT" 모델이 "짧은-CoT" 모델로도 우수한 성능 발휘
- 1.5B 모델이 동일한 토큰 예산으로 GPT-4o와 견줄 수 있는 성능 달성
- 테스트 시 계산과 정확도의 세밀한 할당을 가능하게 하는 정밀한 길이 제어
2. Related Work
- 대형 언어 모델에서 스케일링: 계산이 증가할 수록 성능이 높아짐.
기존 방법: BoN, Tree, O1/R1과 같이 긴 chain of thought 생성 - 대형 언어 모델에서 길이 제어: 길이를 명시적으로 제어.
- 추론 작업을 위한 길이 제어: 상대적으로 미탐색으로 남아 있음.
- Arora&Zanette: 효율성을 위한 짧은 추론 체인 강조 -> 사용자가 명시한 토큰과, 생성된 토큰의 길이가 매칭이 안됨
- S1: 예산 강제 방식으로 -> 갑자기 추론 중간에 잘리는 경우가 많음. 특수 토큰의 반복적 사용이 많고, 최적이 아닌 추론 패턴이 유발된다.
- LCPO: 강화학습을 사용해 모델이 프롬프트에 따라 동적으로 추론 할당.
3. Methodolgy
현재 reasoning language model들은 생성된 reasoning trace의 길이를 제어하는 방법은 없음.
이 연구에서는 프롬프트에 제공된 목표로 하는 토큰 길이를 모델의 인풋으로 조건화함으로써 이 한계를 해결함.
- 입력 프롬프트 x와 목표 길이 $n_{gold}$가 주어지면, 모델은 답변의 정확성을 유지하면서 동시에 $|n_{gold} - n_y|$ 절대 차이를 최소화하는 길이 $n_y$의 응답 y를 생성할 것으로 예상함
Length Controlled Policy Optimization
- 세팅: ReasoningModel(LLM), 데이터 $D={(x_i, y_{gold}, i)}^{N_{i=1}}$.
- 여기서 각 데이터는 입력 프롬프트, 최종 답변만 포함함 (중간 reasoning trace는 없음)
- 프롬프트 확장: 길이 제어를 위해 각 프롬프트 $x_i$는 목표 길이도 추가된다
- $x^{new_i}$ = $concat(x_i, "Think for n_{gold, i} tokens")$
- $n_{gold, i}$: $Z(n_{min}, n_{max})$에서 균일하게 샘플링함(ablation에 살펴보면 100에서 4000사이의 토큰을 무작위로 뽑는것으로 나와있음)
- 강화학습 : GRPO + 길이
- $r(y, y_{gold}, n_{gold})$ = $I(y=y_{gold} - \{alpha} |n_{gold} - n_y|$
- I: indicator, n_y: 생성된 출력 길이, $\{alpha}: 정확한 답변 생성과 목표 길이 사이의 균형을 조절하는 값$
- $\{alpha}$: 알파 값이 낮으면, 어느정도 오차를 허용. 알파 값이 높으면 높은 정확성을 요구함.
- 두가지 목적이 있음:
- 짧은 출력을 강요 시 간결한 reasoning trace를 선호하면서 정확한 답변을 생성하도록 모델을 장려
- 더 적은 토큰으로 정확한 답변을 생성할 수 있더라도, 제공된 토큰 수에 맞춰 답을 하도록 강요
Maximum Length Constraint Mode
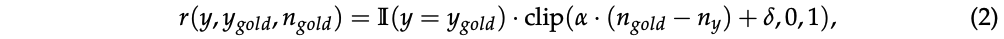
- L1-max 추가로 훈련함: 정확한 토큰수로 생성하는 것보다, 제공된 예산 내에 생성하도록 함.
4. Experimental Setup
- Datasets:
- 훈련: DeepScaleR-Preview-Dataset: AIME, AMC, Omni-Math, STILL에서 추출한 40K개 수학 질문-답변 쌍
- 평가:
- 수학 벤치마크: AIME 2025, MATH, AMC, Olympiad-Bench
- OOD 벤치마크: GPQA, LSAT, MMLU
- 비교 모델: DeepSeek-R1-Distill-Qwen-1.5B, DeepScaleR-1.5B-Preview, DeepScaleR-1.5B-Preview-4K, S1
- Evaluation Protocol
- 첫째, 생성된 토큰 길이 ny와 목표 ngold 사이의 평균 편차를 보고, 모델이 목표 길이를 생성하는지 평가함.
둘째, 다른 목표 길이에서 응답을 생성할 때 성능 평가. 목표 길이는 {512, 1024, 2048, 3600}중에서 선택됨.
- 첫째, 생성된 토큰 길이 ny와 목표 ngold 사이의 평균 편차를 보고, 모델이 목표 길이를 생성하는지 평가함.
- Hyperparameters and Implementation Details:
- DeepScaleR-1.5B-Preview와 동일한 하이퍼파라미터를 채택, 1e-6의 학습률과 128의 배치 크기를 사용, 최대 컨텍스트 길이는 훈련 시 4K 토큰으로 설정되고 평가 중에는 8K 토큰으로 확장, 훈련은 VeRL 프레임워크 사용,nmin = 100 및 nmax = 4000으로 설정, α는 0.0003으로 고정
5. Results and Analysis

L1 significantly outperforms other length-controlled models while maintaining strong performance.
- L1(Exact, Max 두 버전 모두)는 모든 토큰 예산에서 정밀한 길이 제어와 함께 우수한 성능 달성
- S1 대비 512와 1024 토큰 예산에서 100-150% 상대적, 20-25% 절대적 성능 향상
- 로그-선형 스케일링 패턴 보유하나 S1보다 작은 기울기(0.24 vs 0.37)로 낮은 토큰 범위에서 더 효율적
- L1-Max는 상한을 생각하면서, 문제 난이도에 따라 토큰 사용 최적화하여 L1-Exact보다 최대 2배 적은 토큰으로도 더 좋은 성능 달성

L1 generalizes effectively to out-of-domain (OOD) tasks(fig 3)
- GPQA, LSAT와 같은 OOD 일반 reasoning 데이터셋에서도 토큰 예산 증가에 따라 성능 일관적 향상
- MMLU에서는 덜 두드러진 선형 관계(R² = 0.66) 보임 - 지식 중심 질문은 reasoning이 덜 효과적으로 보임.
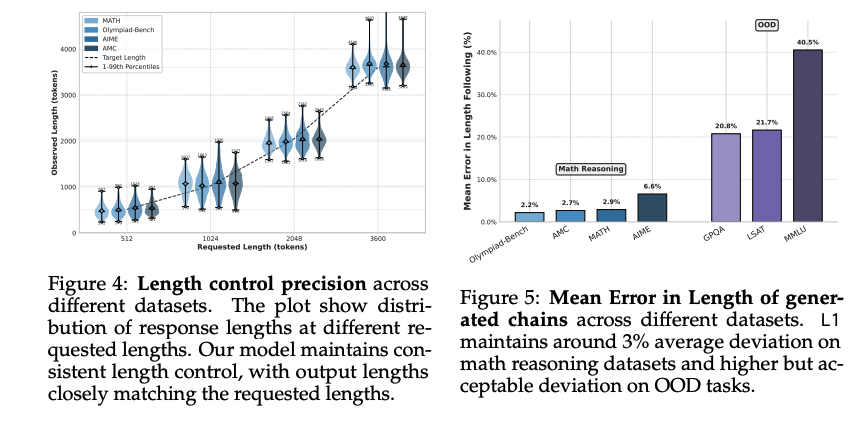
L1 follows length constraints with high precision(fig 4, fig5)
- 수학 reasoning 데이터셋에서 평균 오류 약 3%로 매우 낮음
- OOD 데이터셋에서는 예상대로 더 높은 오류(20-40%)를 보이나 제어되지 않은 모델보다 훨씬 나음
- 확장된 RL 훈련으로 오류를 더 줄일 수 있음을 확인
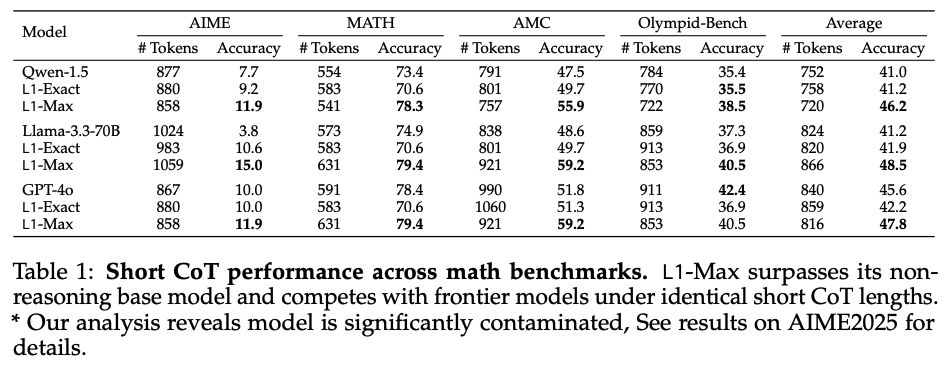
L1 employs distinct reasoning strategies at different token budgets(table 1)
- L1은 동일한 토큰 예산에서 비-reasoning 기본 모델(Qwen)보다 평균 5% 우수
- 놀랍게도 GPT-4o, Llama-3.3-70B와 같은 대형 모델과 비교해도 평균 2% 성능 우수
- 1.5B 모델이 동일 생성 길이에서 최신 대형 모델보다 나은 성능을 보인 첫 사례
- RL 훈련을 통해 long CoT 모델이 효과적인 short CoT 모델로 활용 가능함을 증명
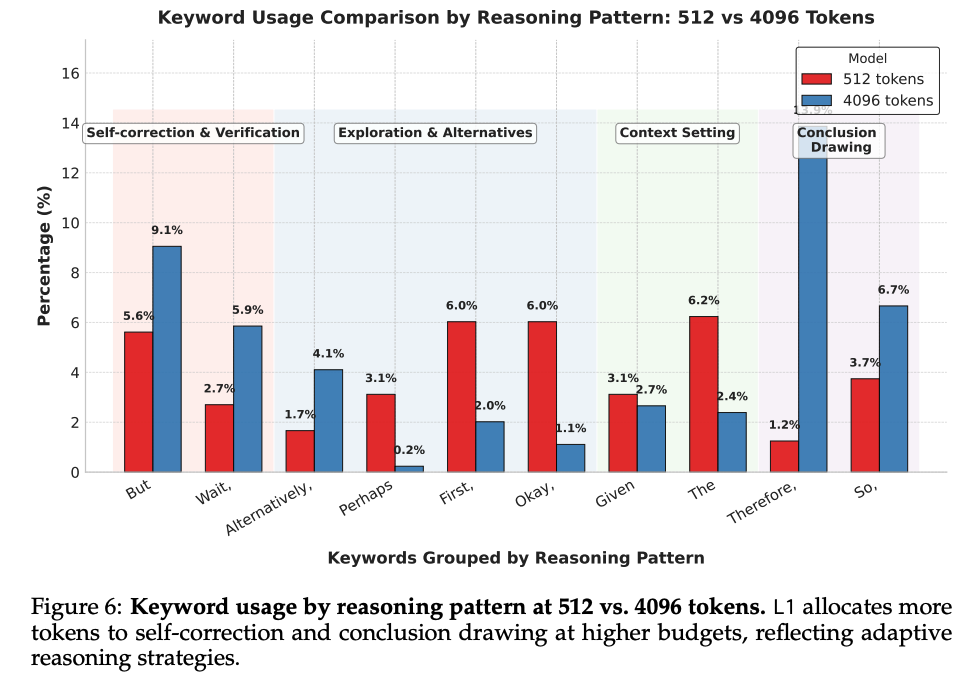
L1 employs distinct reasoning strategies at different token budgets(figure 6)
- 4096 토큰 출력에서는 512 토큰 출력보다 "자기 수정 및 검증" 키워드가 약 2배 더 자주 등장
- 결론 도출 용어는 토큰 예산 증가에 따라 2-10배 빈도 증가
- 대부분의 탐색 관련 키워드는 긴 출력에서 상대적 빈도 감소("Alternatively" 제외)
- thinking 토큰과 solution 토큰의 비율은 다양한 생성 길이에서 비교적 안정적 유지
- 짧은 CoT는 토큰 절약을 위해 간결한 솔루션 제공, 길이 증가 시 최종 솔루션 길이는 안정적으로 유지